Предмет: Алгебра,
автор: yotex48
Найти предел с помощью второго замечательного предела. Ответ должен получиться e^2.
Приложения:
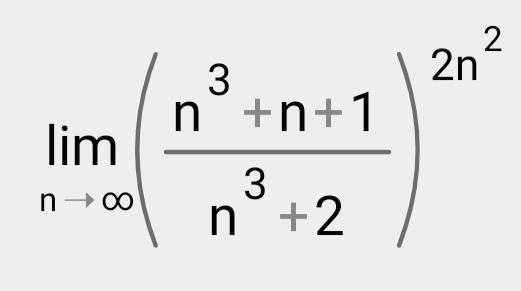
Ответы
Автор ответа:
0
Преобразуем:
Из второго замечательного предела следует: ;
Однако
yotex48:
Здравствуйте. Объясните, пожалуйста, первое равенство в третьей строчке. Как оно получилось?
при n-> infty, константы особой роли не играют. их можно просто убрать
Понял, спасибо!
спасибо
Похожие вопросы
Предмет: Английский язык,
автор: samaarina1988
Предмет: География,
автор: prokipetsliza
Предмет: Химия,
автор: evgeshalovegordeeva
Предмет: Химия,
автор: EnderRider
Предмет: Математика,
автор: Твайлайт1111