Предмет: Математика,
автор: amlansk
Упростить выражения и найти их значения:
Приложения:
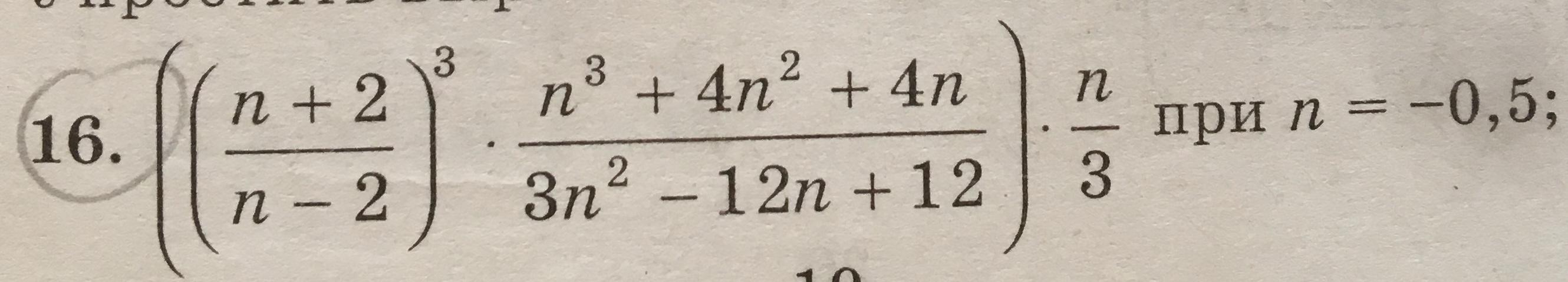
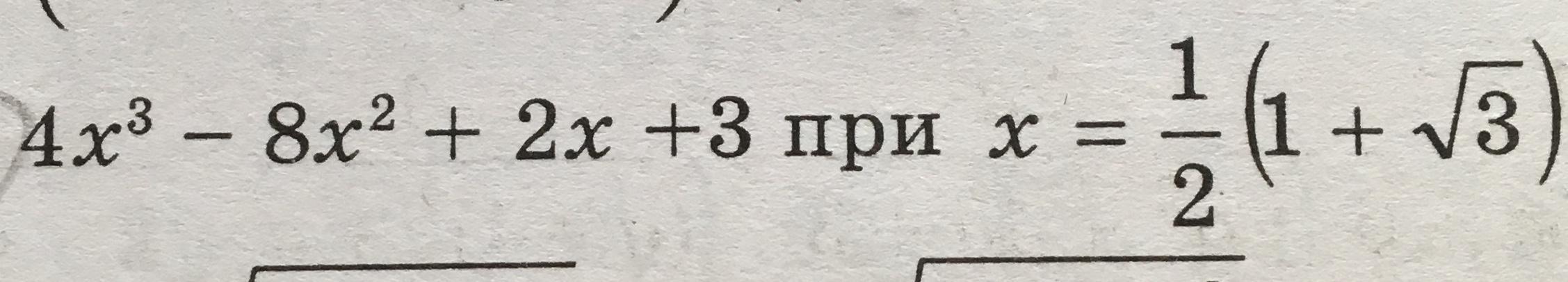
Ответы
Автор ответа:
1
amlansk:
В первом должен получиться ответ -0,6
Опечатка в задании значит.
Похожие вопросы
Предмет: Химия,
автор: veronika132961
Предмет: Математика,
автор: ne4est
Предмет: Математика,
автор: daniipv2009
Предмет: Информатика,
автор: Nita15
Предмет: История,
автор: DIP123456789