Question

построить график функции у= 1/2 модуль х/2 - 2/х модуль закрыть + х/2 +2/х

Answer 1

Раскрываем модуль по определению

Если

(x/2)-(2/x) ≥0,  то | (x/2)-(2/x)|=(x/2)-(2/x)

y=(1/2)· (( x/2)-(2/x))  + (x/2)+(2/x)= (3/2)(x/2)+(1/2)(2/x)=(3x/4)+(1/x)

Если

(x/2)-(2/x)  <0,  то | (x/2)-(2/x)|= - (x/2)+(2/x)

y=(1/2)· (-(x/2)+(2/x))  + (x/2)+(2/x)= (1/2)(x/2)+(3/2)(2/x)=(x/2)+(3/x)

Так как

(x/2)-(2/x) ≥0   ⇒  (x²-4)/x≥0  ⇒ при  x∈[-2;0)U([2;+∞)

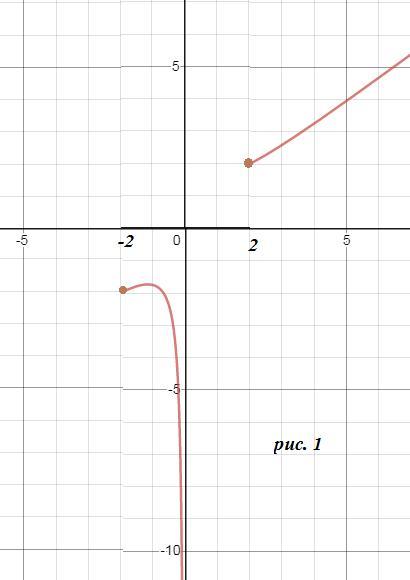
строим график y=(3x/4) + (1/x)  на [-2;0)U([2;+∞)

рис. 1

(x²-4)/x < 0  ⇒ при  x∈ (-∞;-2)U(0;2)

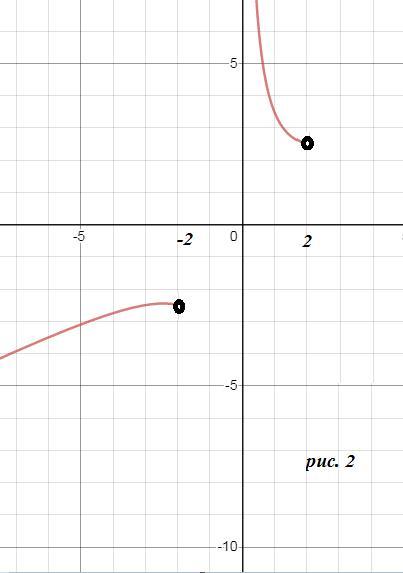
на (-∞;-2)U(0;2)  строим график y=(x/2)+(3/x)

рис. 2

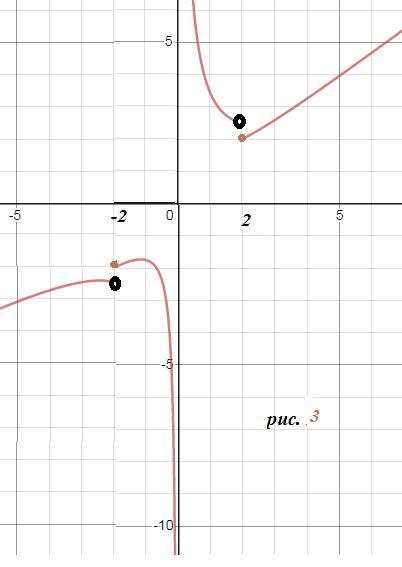
Окончательный график рис. 3