Question

Постройте график функции y = |x|x + 3|x| - 5x. Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

Answer 1

Ответ:

Объяснение:

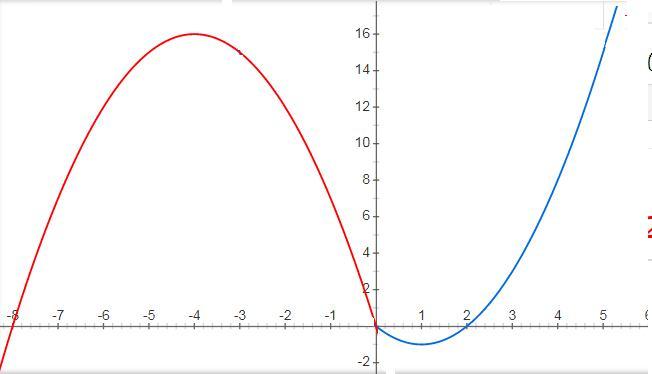
1) при x≥0 IxI=x

y=x²+3x-5x=x²-2x

координаты вершины

х₀=1; y₀=-1

∩ c OX  y=0 x(x-2)=0; x₁=0 ; x₂=2

∩ c OY  x=0 y=0

2) при x<0 IxI=-x

y=-x²-3x-5x=-x²-8x

координаты вершины

х₀=-4; y₀=-16+32=16

∩ c OX  y=0  -x(x+8)=0; x₁=0 ; x₂=-8

∩ c OY  x=0 y=0

3) y = m имеет с графиком ровно две общие точки когда проходит через вершины парабол

m={-1;16}