Предмет: Алгебра,
автор: lerabalueva19
Вычислить предел функции, используя умножение на сопряженное выражение
Приложения:
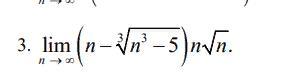
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Старшая степень числителя равна 3/2, а старшая степень знаменателя равна 2. Следовательно, при стремлении n к бесконечности, знаменатель растёт быстрее числителя и предел равен 0.
Похожие вопросы
Предмет: Математика,
автор: tereshkofleshka
Предмет: Математика,
автор: alexandra22841
Предмет: Физика,
автор: katiabruslinovska200
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: medisha1