Question

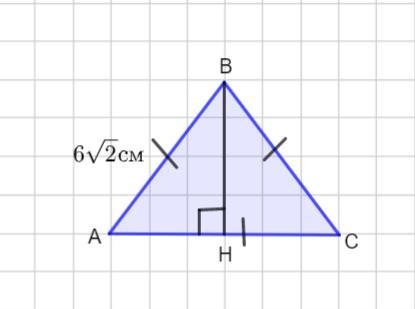
знайти площу рівностороннього трикутника сторона якого дорівнює 6√2 см​

Answer 1

Ответ:

Площадь равностороннего треугольника равна 18√3 см².

Пошаговое объяснение:

Найти площадь равностороннего треугольника, сторона которого равна 6√2 см.

1 способ.

Найдем площадь равностороннего треугольника по формуле

$S =\dfrac{a^{2} \sqrt{3} }{4} ,$   где  a- сторона равностороннего треугольника.

По условию а = 6√2 см.

Тогда площадь будет равна

$S =\dfrac{(6\sqrt{2}) ^{2} \sqrt{3} }{4} =\dfrac{36\cdot2 \sqrt{3} }{4} =\dfrac{4\cdot9\cdot2\sqrt{3} }{4} =18\sqrt{3}$  см ².

2 способ.

Все углы равностороннего треугольника равны по 60°.

Найдем площадь треугольника как полупроизведение двух его сторон на синус угла между ними.

$S =\dfrac{1}{2} \cdot AB \cdot BC \cdot sin B;\\\\S =\dfrac{1}{2} \cdot 6\sqrt{2} \cdot 6\sqrt{2} \cdot sin 60^{0}=3\sqrt{2} \cdot 6\sqrt{2} \cdot \dfrac{\sqrt{3} }{2} =3\sqrt{2} \cdot3\sqrt{2} \cdot \sqrt{3} =9\cdot2\cdot \sqrt{3}=18\sqrt{3}$ см ².

3 cпособ

Найдем площадь треугольника как полупроизведение стороны на высоту, проведенную к данной стороне.

Проведем высоту ВН. В равностороннем треугольнике она является медианой. Поэтому АН=НС =6√2 : 2 = 3√2 см.

Рассмотрим ΔАВН - прямоугольный.

Найдем высоту ВН по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB^{2} =AH^{2} +BH^{2} ;\\BH^{2} =AB^{2} -AH^{2};\\BH= \sqrt{AB^{2} -AH^{2}} ;\\BH= \sqrt{(6\sqrt{2} )^{2} -(3\sqrt{2} )^{2} } =\sqrt{36\cdot2-9\cdot2} =\sqrt{2\cdot(36-9)} =\sqrt{2\cdot27} =\sqrt{2\cdot3\cdot9} =\\=3\sqrt{6}$

Тогда площадь будет

$S =\dfrac{1}{2} \cdot AC \cdot BH ;\\\\S =\dfrac{1}{2} \cdot 6\sqrt{2} \cdot 3\sqrt{6} =9\sqrt{12} =9\sqrt{4\cdot3} =9\cdot2\sqrt{3} =18\sqrt{3}$  см ².

#SPJ5