Предмет: Математика,
автор: plnpnk
ПОЖАЛУЙСТА!!!
Помогите выполнить действия над комплексным числом
Приложения:

Ответы
Автор ответа:
0
Найдем тригонометрическую форму числа
Модуль числа равен √((3/2)²+(√3/2)²)=√(9/4+3/4)=√3
аргумент φ комплексного числа определяется из формул
cosφ=(3/2):√3=√3/2
sinφ(-√3/2):√3=-1/2 с точностью до слагаемого вида 2πк, где к - любое целое. Наименьший неотрицательный угол, удовлетворяющий вспомогательному уравнению tgφ=модулю (частного (-√3/2:(3/2)))=
√3/3; комплексное число находится в 4 квадранте, поэтому
φ=2π-π/6=11π/6
Итак, в тригонометрической форме записи число принимает вид
√3*(сos11π/6+isin11π/6),возведем его в шестую степень
√3*(сos11π/6+isin11π/6)⁶=(√3)⁶((сos(6*(11π/6))+isin(6*(11π/6))=
27(cos11π+isin11π)=27(cosπ+isinπ)=-27
Автор ответа:
0
Ответ:
Всё во вложении.
P.S. тема сложная поэтому ОЧЕНЬ ПОДРОБНО объяснил.
Приложения:


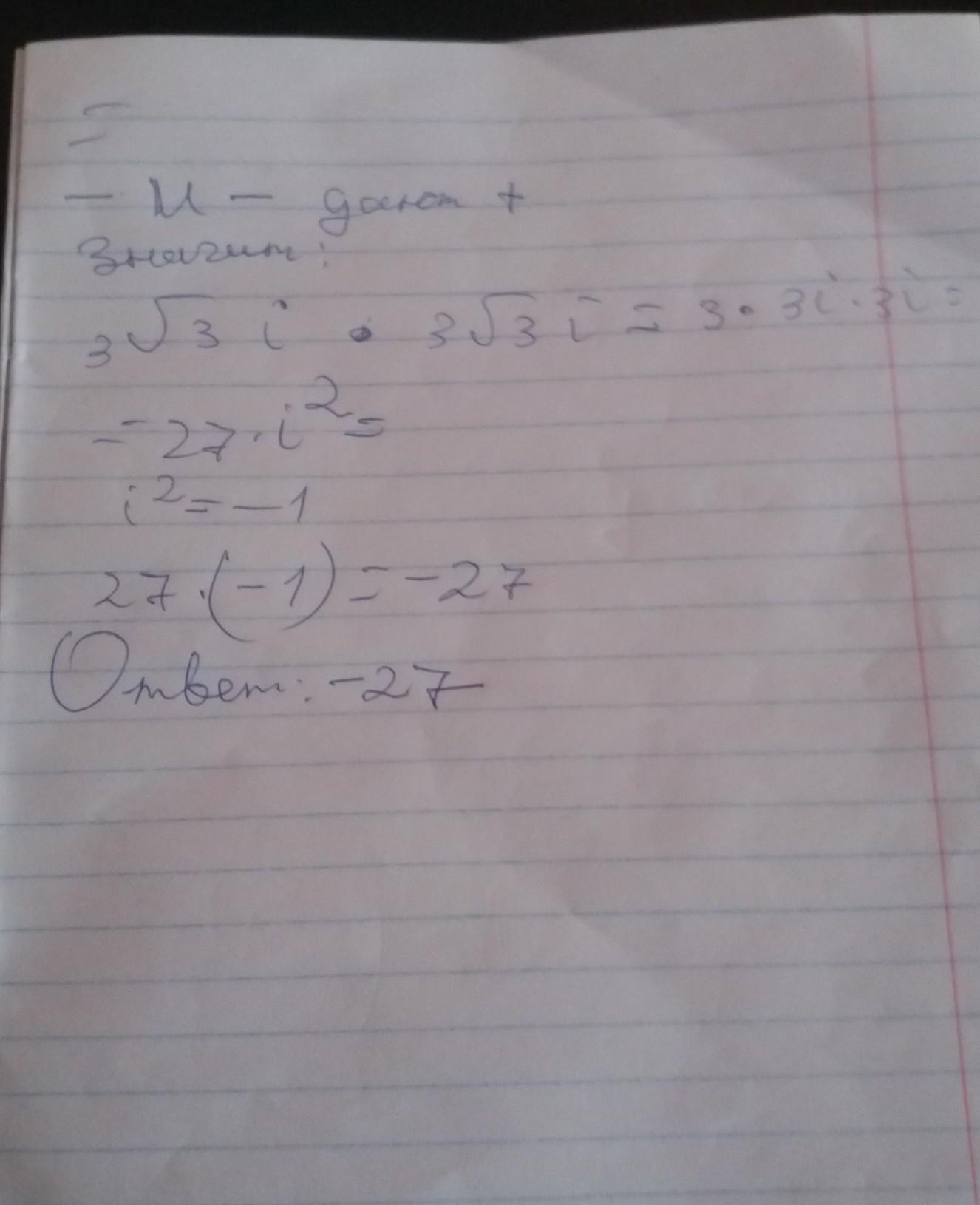
Похожие вопросы
Предмет: Английский язык,
автор: modyle442
Предмет: Русский язык,
автор: edrenkinakhristina00
Предмет: Английский язык,
автор: Kolakon553
Предмет: История,
автор: zlycha