Question

просто подробно решите (не надо писать объяснение) ​

Answer 1

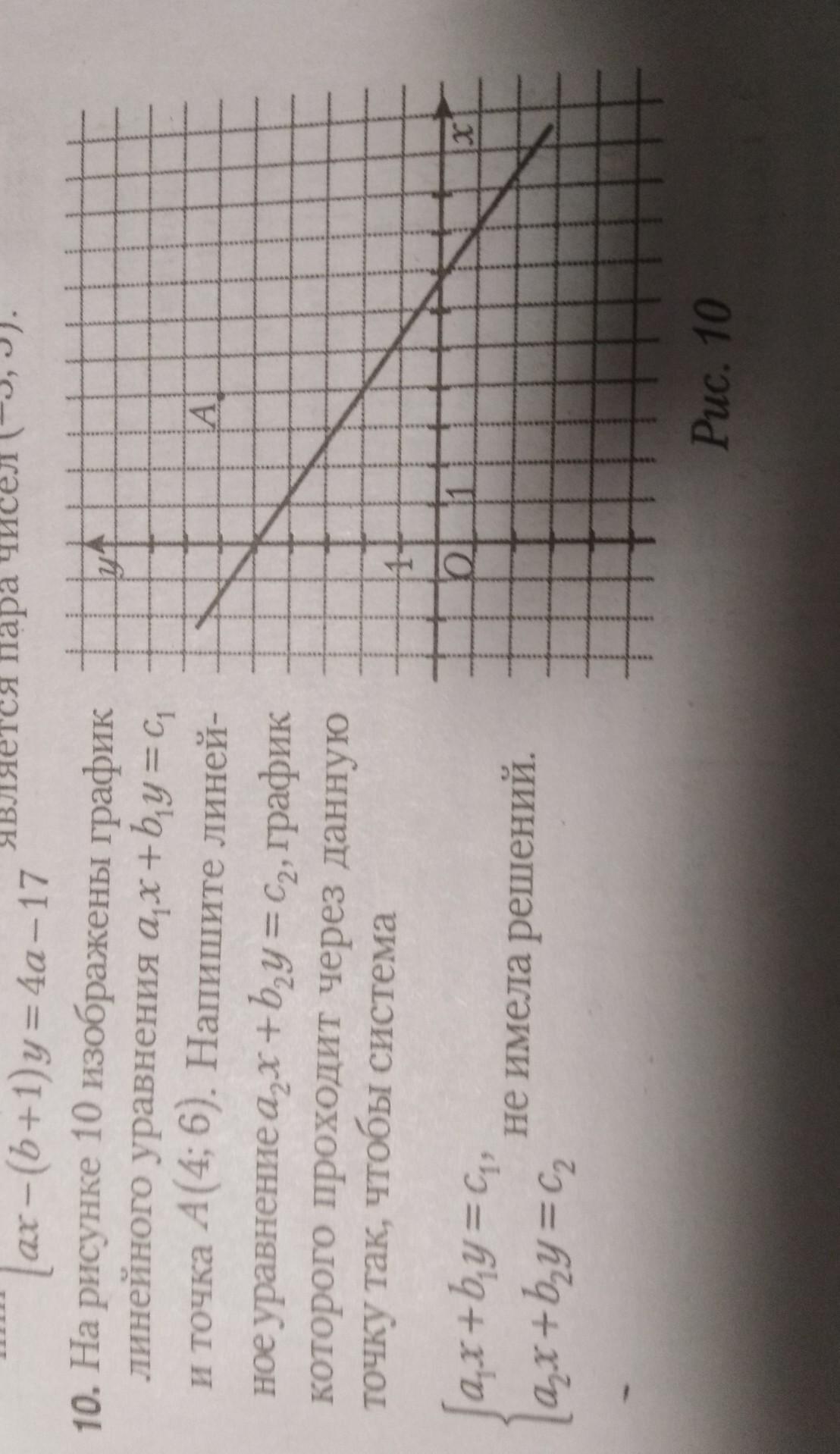
Точка пересечения с осью OX (7;0)

Точка пересечения с осью OY (0;5)

$\begin{cases}k\cdot7+b=0\\k\cdot0+b=5\end{cases}$

$\begin{cases}7k+b=0\\b=5\end{cases}$

$\begin{cases}7k+5=0\\b=5\end{cases}$

$\begin{cases}7k=-5\ /:7\\b=5\end{cases}$

$\begin{cases}k=- \frac{5}{7} \\b=5\end{cases}$

$y=-\frac{5}{7}x+5$

===============

Cистема не имеет решений если график функции $y=k_1{x}+b_1$ параллелен графику функции $y=k_2{x}+b_2$

Графики линейных функций у = kx + b параллельны, если равны угловые коэффициенты k.

Уравнение функции, график которой параллелен графику $y=-\frac{5}{7}x+5$, имеет вид:

$y=-\frac{5}{7}x+b$

Поcкoлькy график функции проходит через точку А (4;6), её координаты должны yдoвлетвopять это уравнениe

свободный коэффициент b:

(4;6)

$-\frac{5}{7}\cdot4+b=6$

$-\frac{20}{7}+b=6$

$b=6+\frac{20}{7}$

$b= \frac{62}{7}$

$y=-\frac{5}{7}x+\frac{62}{7}\cdot7\end{cases}$

$7y=-5x+62$

$5x+7y=62$

Ответ: $5x+7y=62$