Предмет: Геометрия,
автор: Diana818758
Условие: медиана проведенная из вершины прямого угла треугольника равна половине гипотенузе
Дано:треугольник ABC, Угол B=90.
BM медиана
Доказать: BM=1/2 AC
Ответы
Автор ответа:
3
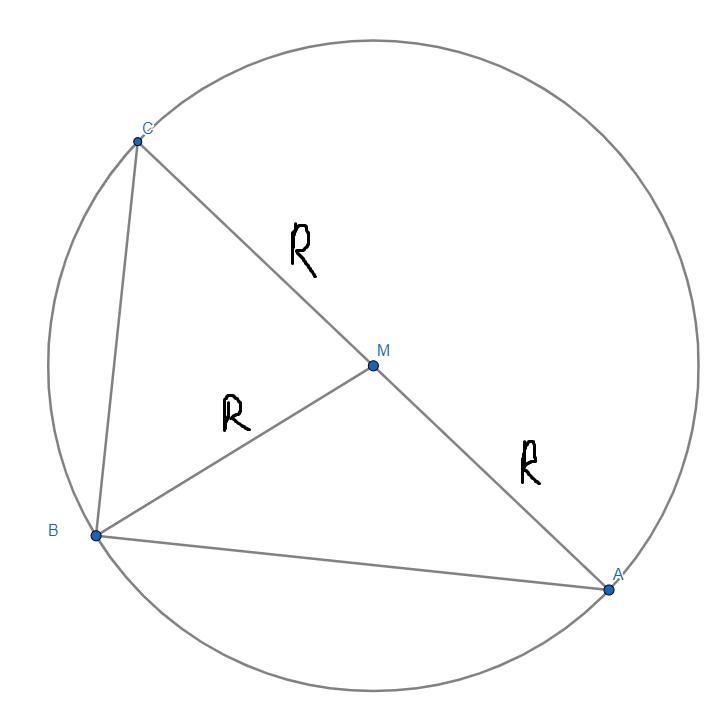
Опишем около треугольника окружность, так-как угол B прямой, он будет опираться на дугу 180°, значит он опирается на диаметр.
Центр окружности лежит на середине AC так-как туда падают серединные перпендикуляры треугольника.
значит:
AM=MC=BM как радиусы окружности.
отсюда:
Приложения:
Автор ответа:
0
Ответ:
ВМ =1/2АС
Объяснение:
Впишим прямоугольный треугольник в круг.
Так как медиана находиться на центре окружности(т. О) , то т. О делит медиану на 2 радиуса, то есть АО =ОС. ВМ- медиана, то есть тоже радиус, и значит О совпадает с М. ВМ=АО=СО, ВМ =1/2АС
Похожие вопросы
Предмет: Литература,
автор: vitcongo9197
Предмет: Математика,
автор: wsbksscewje6661
Предмет: Литература,
автор: dinara17982
Предмет: Математика,
автор: Сметана11
Предмет: Математика,
автор: radik12331