Question

в треугольнике abc угол abc равен углу acb биссектрисы cd и bk пересекаются в точке f. докажите что треугольник fbc равнобедренный

Answer 1

Ответ: Доказано

Объяснение:

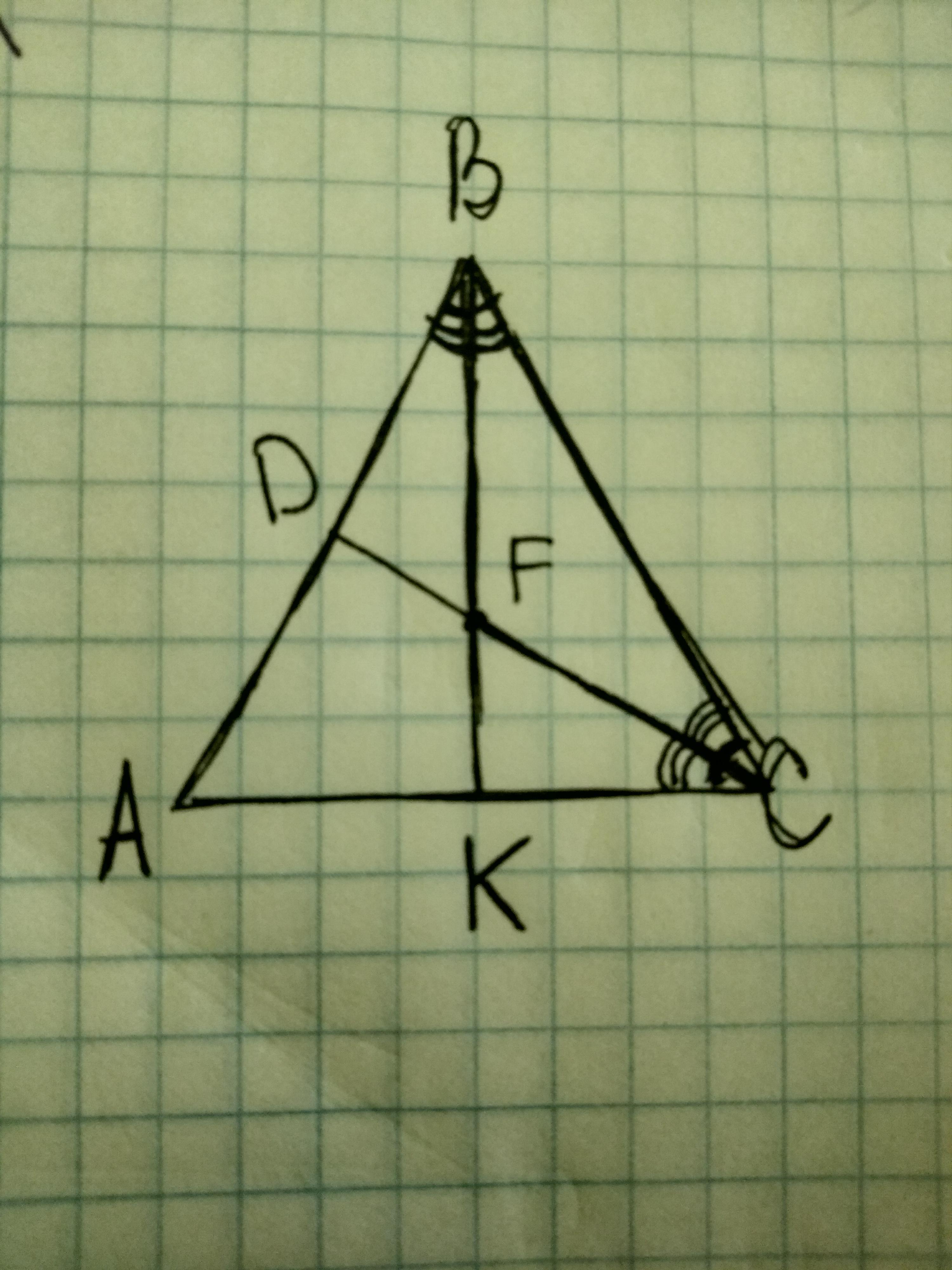
Дан треугольник АВС. Угол АВС равен углу АСВ. ВК, СD-биссектрисы, пересекающиеся в точке F. Докажем, что треугольник FBC-равнобедренный.

Угол АВС=углу АСВ. Если в треугольнике два угла при основании равны, то такой треугольник называется равнобедренным. Значит, треугольник АВС-равнобедренный, с основанием СВ.

ВК, СD-биссектрисы. Биссектриса делит угол на два равных угла. Таким образом, угол АВК= углу КВС= углу ВСD= углу DCA. Рассмотрим треугольник FBC. Т.к. в треугольнике FBC два угла при основании равны(КВС=ВСD), то такой треугольник называется равнобедренным. Значит, треугольник FBC-равнобедренный, с основанием ВС.