Предмет: Математика,
автор: batalovaregina
Исследовать сходимость знакоположительных рядов.
Приложения:
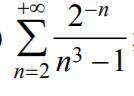
Ответы
Автор ответа:
0
Ответ:
K<1 - ряд сходится по признаку Коши
Пошаговое объяснение:
Воспользуемся радикальным признаком Коши:
=> Ряд сходится
Похожие вопросы
Предмет: Математика,
автор: volkovicaleksandr15
Предмет: Математика,
автор: sofiavajgant
Предмет: Математика,
автор: havwhis
Предмет: Математика,
автор: zsa1
Предмет: Биология,
автор: brain0niarb