Предмет: Алгебра,
автор: BellaL
Помогите, пожалуйста Г)
Буду очень-очень благодарна вам
Приложения:
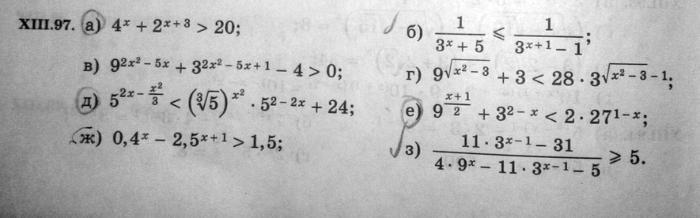
Ответы
Автор ответа:
0
3^-1 = 1/3
умножаем каждый член на 3 и запишем 9 как 3^2
делаем замену t>0 t =
очевидно что корни 9 и 1/3
так как x1 + x2 = -b/a; x1*x2=c/a
при любом х из одз
решение последние 3 строчки
одз
x <= -√3 и x => √3
Ответ x (-√7; -√3]∪[√3;√7)
Похожие вопросы
Предмет: Биология,
автор: doryinocean
Предмет: Физика,
автор: nastyalebedeva9876
Предмет: Геометрия,
автор: tatarenko1897
Предмет: Физика,
автор: 4uwa4ok
Предмет: Литература,
автор: Kat0071