Question

Окружность, вписанная в прямоугольную трапецию, делит точкой касания большую
боковую сторону на отрезки 8 см и 50 см. Найдите периметр трапеции.

Answer 1

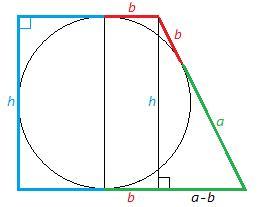
Отрезки большей боковой стороны a=50 и b=8. Отрезки касательных, проведенных из одной точки, равны. Проведем диаметр вписанной окружности, соединив точки касания на основаниях - отсеченные отрезки оснований равны a и b. Опустим высоту из вершины меньшего основания - отсеченный отрезок основания равен a-b. По теореме Пифагора высота равна

h= √((a+b)^2-(a-b)^2) =2√(ab)

Боковая сторона, перпендикулярная основаниям, равна высоте (расстояние между параллельными постоянно). Суммы противоположных сторон описанного четырехугольника равны, периметр равен

P= 2(2√(ab)+(a+b)) =2(√a+√b)^2

P= 2(√50+√8)^2 =2(7√2)^2 =196