Предмет: Математика,
автор: Громова203
Найти производную функции
Приложения:
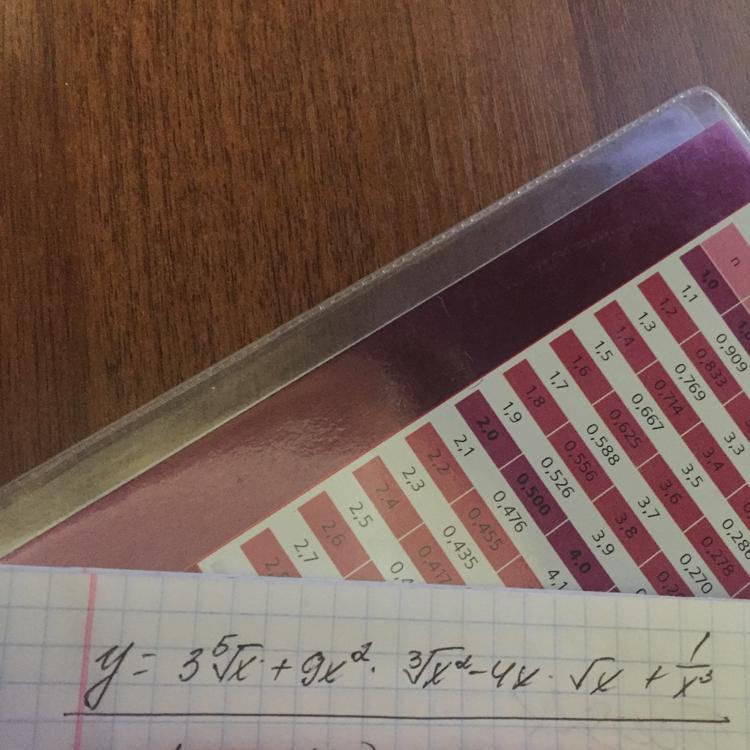
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Громова203:
Объясните ,пожалуйста, как в предпоследнем примере получились степени
По формуле (x^n)'=n*x^(n-1)
т.е. если надо найти производную (3х^2)'=3*2x^(2-1)=6x^1=6x
Спасибо, поняла
Помогите, пожалуйста, и с другими
Похожие вопросы
Предмет: Физика,
автор: alinasylkina29
Предмет: Английский язык,
автор: nolik1001r
Предмет: Математика,
автор: miroslavalevcenko487
Предмет: География,
автор: Аноним
Предмет: География,
автор: Аноним