СрОчНо. Матан. Исследование и построение графиков функций с помощью производной

Ответы
1. Область определения функции - ограничений нет, х ∈ Z.
2. Точки пересечения функции с осями координат.
С осью Оу при х = 0, у = -5.
С осью Ох при у = 0. Надо решить такое уравнение: -х³ + 3х - 5 = 0.
Для вычисления корней кубического уравнения используются формулы Кардано.
Для начала уравнение приводится к виду:
y³ + py + q = 0. Ответ: 1 точка х = -2,279.
4. Производная равна: y' = -3х +3
5. 6. Промежутки возрастания, убывания, экстремумы функции.
Приравниваем производную нулю: -3х² + 3 = -3(х² - 1) = 0.
Отсюда имеем 2 критические точки: х = 1 и х = -1.
Находим знаки производной на полученных промежутках:
х = -2 -1 0 1 2
y' = -9 0 3 0 -9.
Минимум в точке х = -1, у = -7 (переход с - на +),
максимум в точке х = 1, у = -3 (переход с + на -).
Функция возрастает при y' > 0, это промежуток (-1; 1).
Убывает (-∞; -1) ∪ (1; +∞).
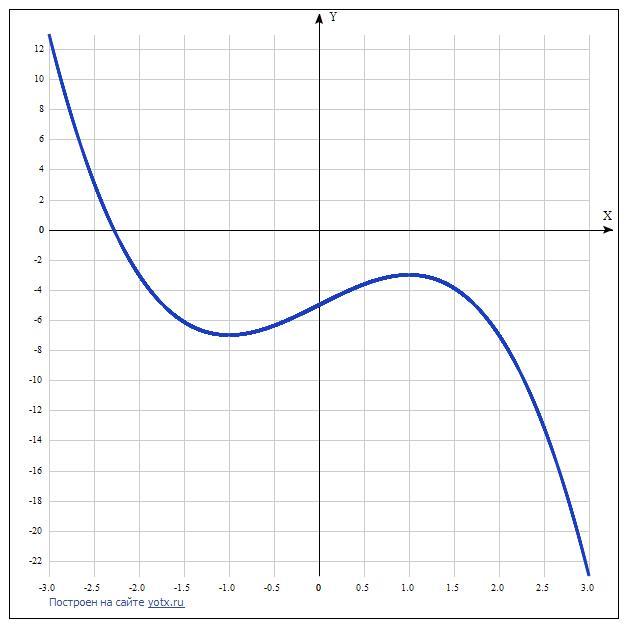
7. Построение графика.
Таблица точек:
x y
-3.0 13
-2.5 3.1
-2.0 -3
-1.5 -6.1
-1.0 -7
-0.5 -6.4
0 -5
0.5 -3.6
1.0 -3
1.5 -3.9
2.0 -7
2.5 -13.1
3.0 -23.