Предмет: Геометрия,
автор: 10doctorwho
СРОООЧНО! ПОМОГИТЕ РЕШИТЬ, КТО СМОЖЕТ
СРОООЧНО! ПОМОГИТЕ РЕШИТЬ, КТО СМОЖЕТ РЕШИТЬ ЗАДАЧИ, ТОМУ ЕЩЕ 20 БАЛЛОВ ОТДАМ!!
Приложения:

Ответы
Автор ответа:
0
№1 строим отрезок(вектор) x=2 см. Стрелочка должна быть вправо
что бы построить вектор 3x, нужно 2*3=6 см. Строим вектор равный 6 см (стрелка вправо)
-2x -2*2=-4 строим вектор равный 4см (стрелка влево)
1/2x 1/2*2=1см вектор равный 1 см. (стрелка вправо)
№2 AK:KB=2:1
АК=23 *вектор АВ =2/3*вектор a
диагонали параллелограмма пересекаются и в точке пересечения делятся пополам, вектор ОС=12 * вектор АС
по правилу параллелограмма для векторов
ОС=12* (АВ+AD)=(a+b)/2 вектор
СК=вектор СА+ вектор АК= -вектор АС+23 *вектор АВ=-(вектор АВ+вектор АD)+23 *вектор АВ =-13*вектор а+вектор b=-a/3-b
вектор СК=-a/3-b
что бы построить вектор 3x, нужно 2*3=6 см. Строим вектор равный 6 см (стрелка вправо)
-2x -2*2=-4 строим вектор равный 4см (стрелка влево)
1/2x 1/2*2=1см вектор равный 1 см. (стрелка вправо)
№2 AK:KB=2:1
АК=23 *вектор АВ =2/3*вектор a
диагонали параллелограмма пересекаются и в точке пересечения делятся пополам, вектор ОС=12 * вектор АС
по правилу параллелограмма для векторов
ОС=12* (АВ+AD)=(a+b)/2 вектор
СК=вектор СА+ вектор АК= -вектор АС+23 *вектор АВ=-(вектор АВ+вектор АD)+23 *вектор АВ =-13*вектор а+вектор b=-a/3-b
вектор СК=-a/3-b
Приложения:
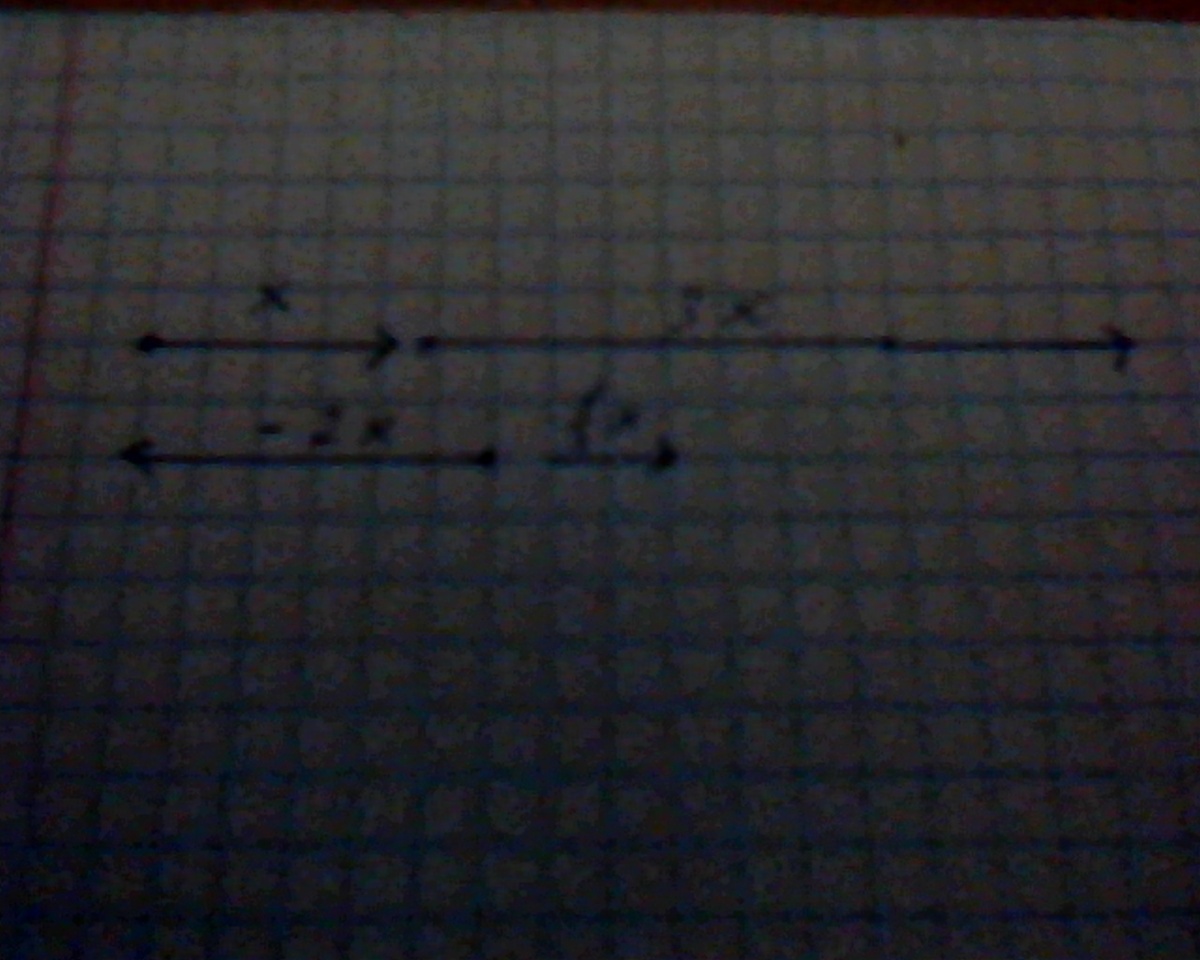
Похожие вопросы
Предмет: Алгебра,
автор: wwwabvgd01
Предмет: Математика,
автор: kamila5579
Предмет: География,
автор: vinervin76
Предмет: Физика,
автор: Ирэн1234
Предмет: Физика,
автор: mama0andrei