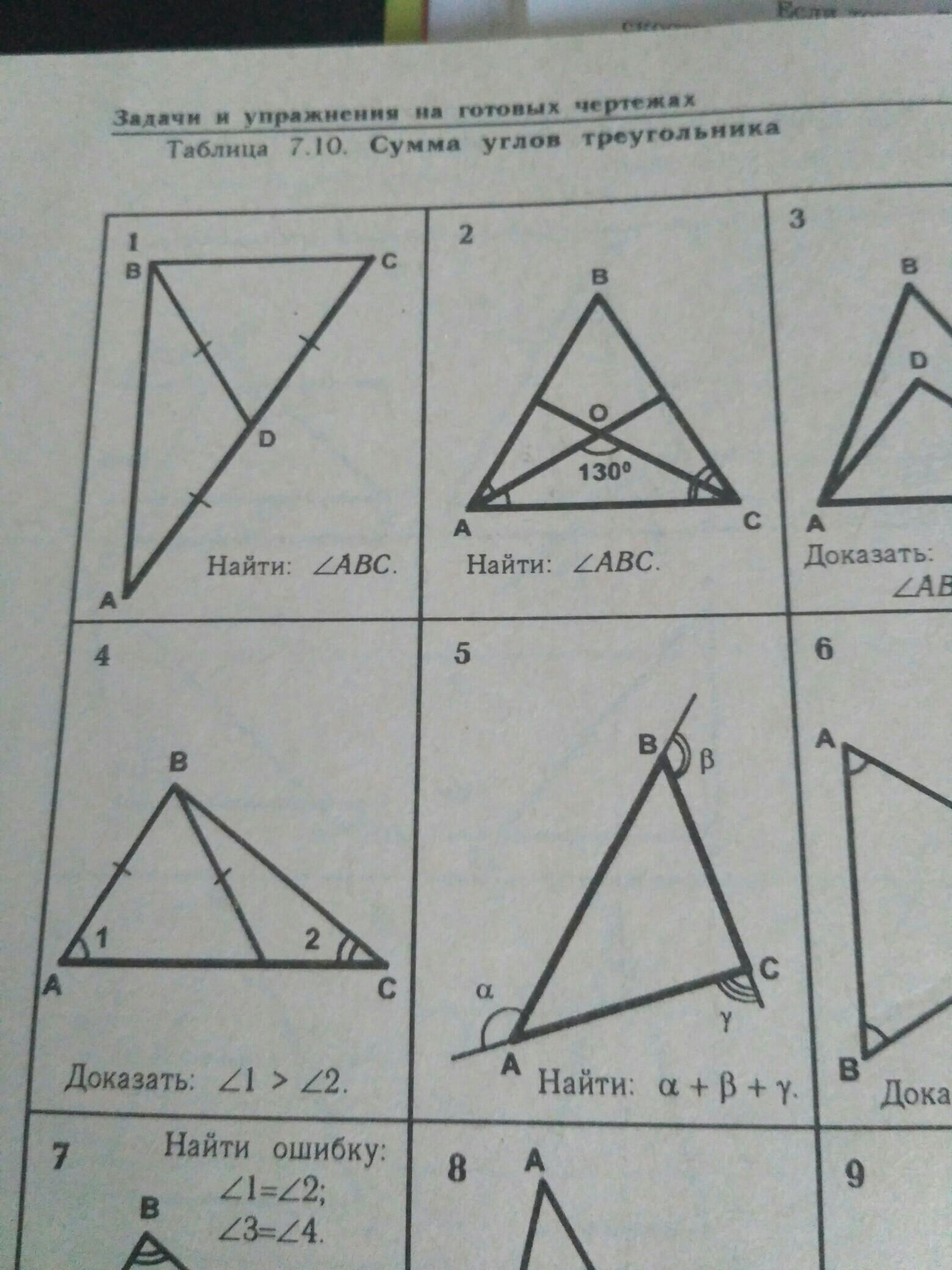
помогите решить 1,2,4,5 задачу плиз
Ответы
1.
Треугольники ABD и BCD равнобедренные.
В треугольнике ABD ∠ABD = ∠BAD = (180°-∠ADB)/2
В треугольнике BCD ∠CBD = ∠BCD = (180°-∠BDC)/2
Угол ABC = ∠ABD+∠CBD = (180°-∠ADB)/2+(180°-∠BDC)/2 = (180°+180°-∠ADB-∠BDC)/2 = (360°-(∠ADB+∠BDC))/2
∠ADB+∠BDC = 180°, т.к. это смежные углы. Тогда
∠ABC = (360°-180°)/2 = 180°/2 = 90°
2.
Пусть ∠OAC = x°. Тогда из ΔACO ∠ACO = 180°-130°-x = 50°-x°.
В треугольнике ABC ∠ABC = 180°-∠BAC-∠BCA = 180°-2·∠OAC-2·∠ACO = 180°-2x-2·(50°-x) = 180°-2x-100°+2x = 80°
4.
Поставьте точку D.
Треугольник ABD равнобедренный, ∠BAD = ∠BDA. Так как сумма углов треугольника равна 180°, углы ∠BAD и ∠BDA - острые (иначе сумма углов будет больше 180°).
∠BDA+∠BDC = 180°, т.к. это смежные углы.
Поскольку ∠BDA острый, угол ∠BDC - тупой. В треугольнике тупой угол может быть только один. Это означает, что в треугольнике BDC ∠BDC - наибольший, а в треугольнике против бОльшего угла лежит бОльшая сторона. То есть BC > BD.
В треугольнике ABC AB > BD, значит, ∠1 > ∠2.
5.