Question

Даю 50 баллов! Мне СРОЧНО надо!!!
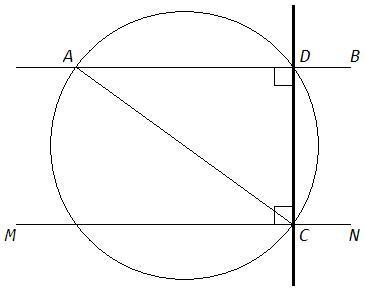
Проведем через точку А прямую AB параллельно прямой MN. Возьмём на MN некоторую точку C. На отрезке АC, как на диаметре построим полуокружность Пусть D точка пересечения этой полуокружности с перпендикуляром к прямой МN проходящей через точку C. Докажите что точка D лежит на прямой ВА. ​

Answer 1

Точка D лежит на окружности. Вписанный угол ADC - прямой, так как опирается на диаметр AC.

CD⊥AD, CD⊥MN => AD||MN

AB||MN. Через точку (A) вне данной прямой (MN) можно провести только одну прямую, параллельную данной. Следовательно, прямые AD и AB совпадают, точка D лежит на AB.