Предмет: Математика,
автор: alex5266
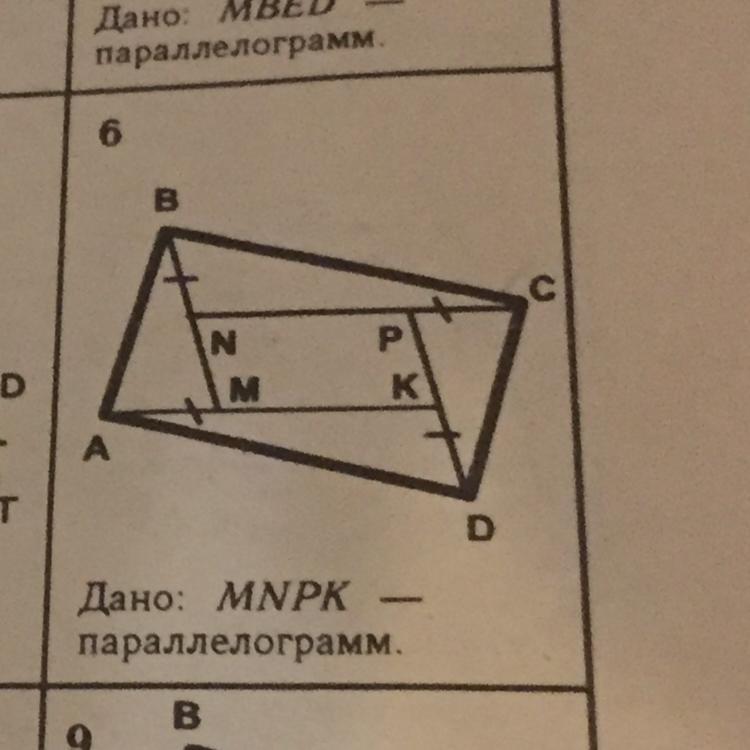
Дано: MNPK — параллелограмм.
Доказать: ABCD — параллелограмм.
(Рис.6)
Помогите, пожалуйста! Подробно, пожалуйста.
Приложения:
Ответы
Автор ответа:
6
Т.к МNPK — параллелограмм, то угол NMK= угол NPK и угол MNP= угол MKP (как противолежащие)
Т. К угол NMK= угол NPK, то угол АМВ= угол СРD (сумма смежных углов = 180•)
Т.к уголMNP= угол MKP, то угол BNC= угол AKD.
Рассмотрим треугольники АМВ и DPC
Т.к AM=MB=DK=PC, угол АМВ= угол СРD, то треугольник равны по 1 признаку равенства треугольников.
Рассмотрим треугольники BNC и AKD
Т.к BN=KD, NC=AK(NP=MK, PC=AM), то треугольники эти равны по 1 признаку
Т.к треугольники BNC=AKD и треугольники АМВ=DPC, то AB=DC, AD=BC.
Значит, АВСD — параллелограмм
Т. К угол NMK= угол NPK, то угол АМВ= угол СРD (сумма смежных углов = 180•)
Т.к уголMNP= угол MKP, то угол BNC= угол AKD.
Рассмотрим треугольники АМВ и DPC
Т.к AM=MB=DK=PC, угол АМВ= угол СРD, то треугольник равны по 1 признаку равенства треугольников.
Рассмотрим треугольники BNC и AKD
Т.к BN=KD, NC=AK(NP=MK, PC=AM), то треугольники эти равны по 1 признаку
Т.к треугольники BNC=AKD и треугольники АМВ=DPC, то AB=DC, AD=BC.
Значит, АВСD — параллелограмм
Похожие вопросы
Предмет: Математика,
автор: darinaana76
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: isendzhanovasanali
Предмет: Физика,
автор: vvvikyla
Предмет: Математика,
автор: Аноним