Question

В сборочный цех завода поступили однотипные детали изготовленные на трех автоматах. Известно что первый автомат дает 3%, второй-1%, а третий-2% брака. Найти вероятность попадания на сборку годной детали, если с каждого автомата в цех поступило соответственно 500, 200, и 300 деталей​

Answer 1

Пошаговое объяснение:

Два события выбрать случайную деталь и чтобы она оказалась годной.

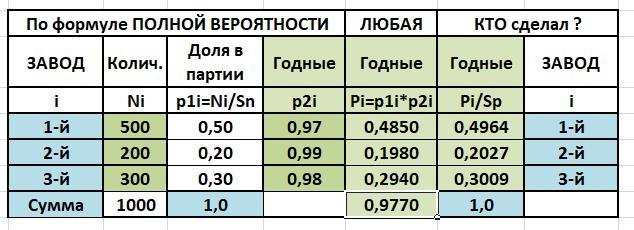
Расчет сведен в таблицу в приложении.

Вероятности Р1i для каждого автомата находим по количеству деталей в партии. Всего деталей в партии - 1000 шт.

Вероятность годных деталей - Р2i находим по формуле:

p2(i) = 1 - q(i)

Вероятность нашего события:  от 1-го автомата И годна ИЛИ от 2-го И годная ИЛИ от 3-го И годная - сумма произведений.

Р(А) = 0,5*0,97 + 0,2*0,99 + 0,3*0,98 = 0,977 - вероятность годной - ответ.

По формуле Байеса можно узнать, что с вероятностью 0,4954 это будет деталь с 1-го автомата.