Предмет: Алгебра,
автор: s201141181s
Решите уравнение. 50 баллов
Приложения:
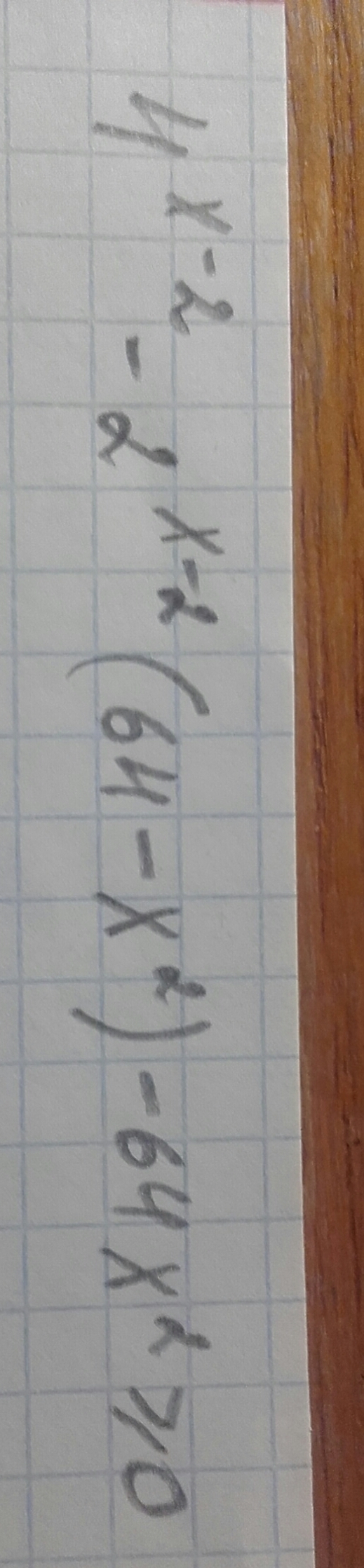
Ответы
Автор ответа:
1
4ˣ⁻² - 2ˣ⁻²•(64 - х²) - 64х² ≥ 0
Расскроем скобки, сгруппируем слагаемые и разложим на множители:
4ˣ⁻² - 2ˣ⁻²•64 + 2ˣ⁻²•х² - 64х² ≥ 0
(4ˣ⁻² - 2ˣ⁻²•64) + (2ˣ⁻²•х² - 64х²) ≥ 0
2ˣ⁻²•(2ˣ⁻² - 64) + х²•(2ˣ⁻² - 64) ≥ 0
(2ˣ⁻² - 64)•(2ˣ⁻² + х²) ≥ 0
В первой скобке применим метод рационализации: aˣ - aⁿ V 0 ⇔ (a - 1)(х - n) V 0
Вторая скобка строго положительна, так как представляет собой сумму показательной и степенной функции.
2ˣ⁻² - 2⁶ ≥ 0
х - 2 - 6 ≥ 0
х - 8 ≥ 0
х ≥ 8
ОТВЕТ: [ 8 ; + ∞ )
Похожие вопросы
Предмет: Русский язык,
автор: baksa087
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: OCULUSIII
Предмет: Алгебра,
автор: Nastya17Marshmallow
Предмет: История,
автор: ЛуннаяВедьма