Предмет: Алгебра,
автор: artakvarderesy
с обьяснениями!!!!!!!!!!!!!
Приложения:

Ответы
Автор ответа:
0
решение с пояснением на фото
Приложения:
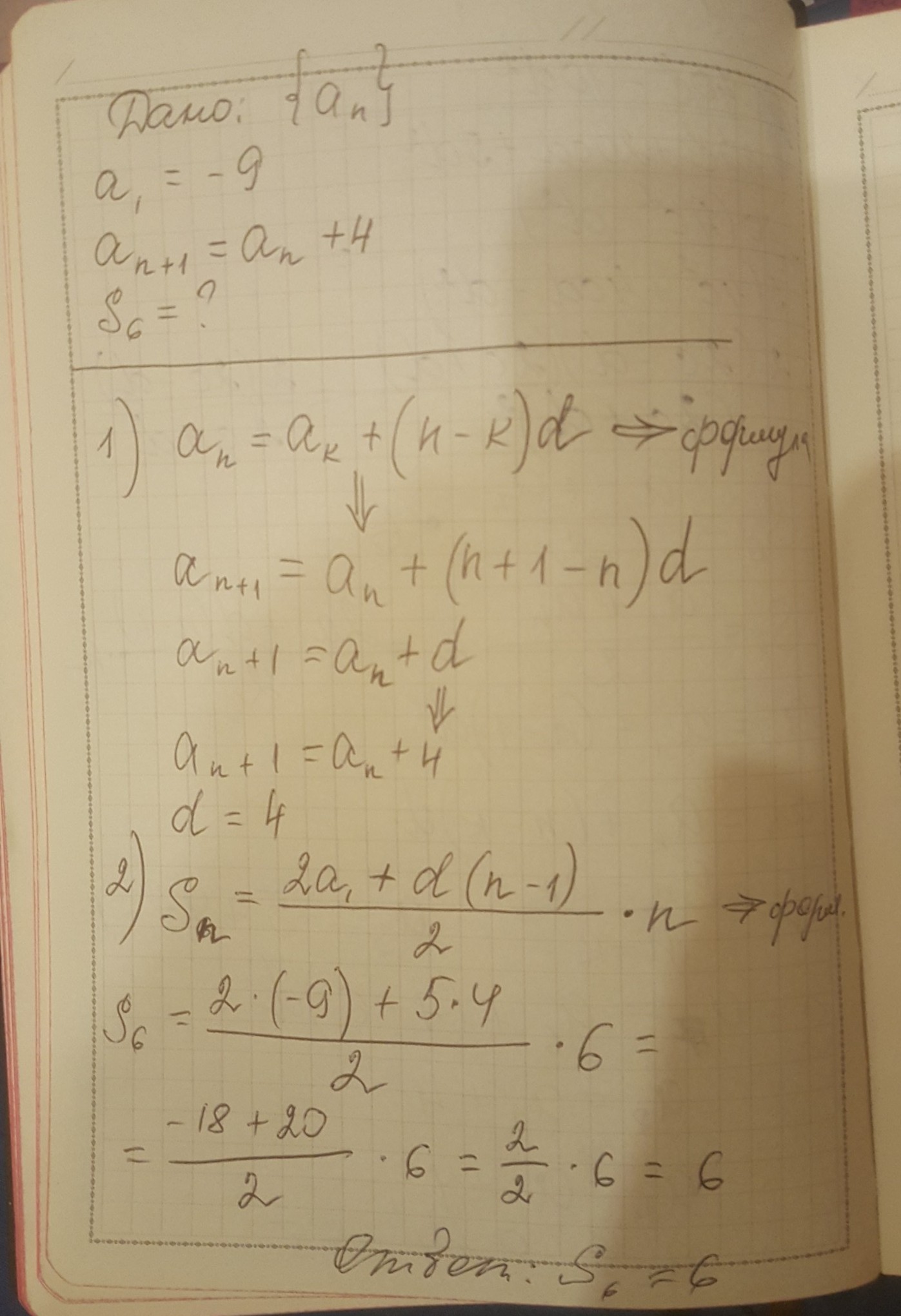
Похожие вопросы
Предмет: Математика,
автор: ObiVoVan28
Предмет: История,
автор: no228338
Предмет: Русский язык,
автор: aknrmyrzagalieva
Предмет: Геометрия,
автор: nikiniki02