Question

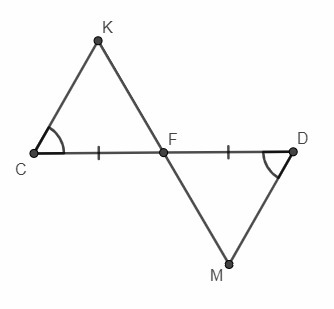
1) Отрезки CD и MK пересекаются вточке F. Причем CF=FD и KCF = FDM. Докажитечто CK = MD

2) Периметр равнобедренного треугольника 24см. Одна из сторон треугольника равна 8см. Найти все стороны треугольника. Два варианта решений.


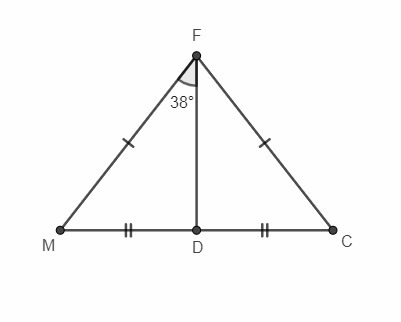
3) В треугольнике MFС FD - медиана, MF = FC. MFD = 38гр. Найти DCF;CFD;DMF;MFC

Answer 1

1. (рисунок в приложении)

Рассмотрим треугольники СКF и DMF:

CF = FD (по условию)

∠KCF = ∠FDM (по условию)

∠CFК = ∠DFM  (вертикальные углы)

Следовательно, ΔСКF = ΔDMF по стороне и прилежащим углам. В равных треугольниках соответствующие стороны равны ⇒  CK = MD, что и требовалось доказать.

2.

Боковые стороны равнобедренного треугольника равны.

а) если основание треугольника равно 8 см, тогда каждая из боковых сторон равна

(24 - 8)/2 = 8 (см)

б) если боковая сторона равна 8 см, тогда основание равно

24 - 8*2 = 8 (см)

Треугольник равносторонний, со стороной 8 см.

3. (рисунок в приложении)

В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

• ∠CFD = ∠MFD = 38° (так как FD - биссектриса)

• ∠MFC = 2∠MFD = 2*38 = 76° (так как FD - биссектриса)

• ΔDCF - прямоугольный (так как FD - высота), тогда:              ∠DCF = 90 - ∠CFD = 90 - 38 = 52°

• ∠DMF = ∠DCF = 52° (так как углы при основании равнобедренного треугольника равны).