Предмет: Алгебра,
автор: sabnab10
метод решения нуженнн
Приложения:
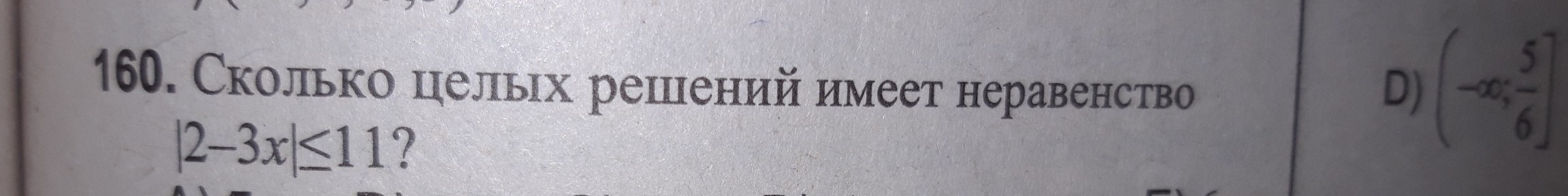
Ответы
Автор ответа:
0
Ответ : 8
[ -3; -2; -1 ; 0; 1; 2; 3 4]
Решение в приложении
Приложения:

Автор ответа:
0
Это опорное неравенство с модулем. Когда переменная есть только внутри модуля, а значит можно раскрыть без определения.
Пример опорных неравенств с модулем:
х - все числа когда существует, вдруг х это 1/х и тогда х не равно 0.
Никогда, модуль всегда не отрицательный.
Случаи строго неравенства рассматривать не буду можно и так догадаться.
Лучше не писать от большего к меньшему и сразу записать следующее.
Найдём ближайшее меньшее, целое число после 13/3. (13/3=4 и 1/3).
Сколько целых значений лежит в промежутке от -3 до 4 включая концы?
|4-(-3)+1|=8.
Ответ: 8.
Похожие вопросы
Предмет: Геометрия,
автор: sofiakasianenko965
Предмет: Математика,
автор: annaromanisin333
Предмет: Геометрия,
автор: shabunkoartur12
Предмет: Математика,
автор: Mедведь