Предмет: Математика,
автор: typik01
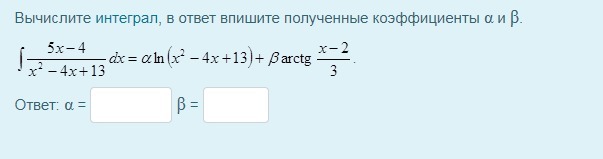
Вычислите интеграл, в ответ впишите полученные коэффициенты α и β.
Приложения:
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Английский язык,
автор: dimavahilevych
Предмет: Геометрия,
автор: qweennn11
Предмет: Алгебра,
автор: melnicukangelina727
Предмет: Математика,
автор: masseffect010kasumi