Question

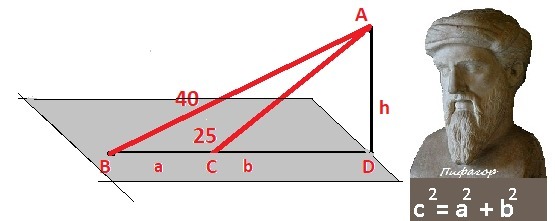
Из точки к плоскости проведены две наклонные длиной 40 см и 25 см. Найдите расстояние от точки до плоскости,если сумма их проекций равна 39 см.

Answer 1

Ответ: 24 см - высота.

Пошаговое объяснение:

Рисунок к задаче в приложении. Расстояние до плоскости - высота AD. Применяем теорему Пифагора.

1) h² = 40² - a² = 1600 - a² - из большого треугольника

2) h² = 25² - b² = 625 - b² -  из малого треугольника.

3) a + b = 39 см - сумма проекций.

Вычитаем уравнения.

4) 1600 - 625 - a² + b² = 0

5) a² - b² = 975 = (a-b)*(a+b) = 39*(a-b)

6) a - b = 975 : 39 = 25 см - разность проекций.

Сложили ур. 3) + 6)

7) 2*a = 39 + 25 = 64 см

8) a = 64 : 2 = 32 - большая  проекция.

Вычисляем катет - высоту -  h.

9) h² = 40² - 32² = 1600 - 1024 = 576.

10) h = √576 = 24 см - высота -  ответ.