Предмет: Геометрия,
автор: daryakartonvezhi
ОС - биссектриса АОВ
угол 1 = 128°, угол 2 = 52°
а) Докажите, что АО=АС
б) Найдите угол АСО
Приложения:
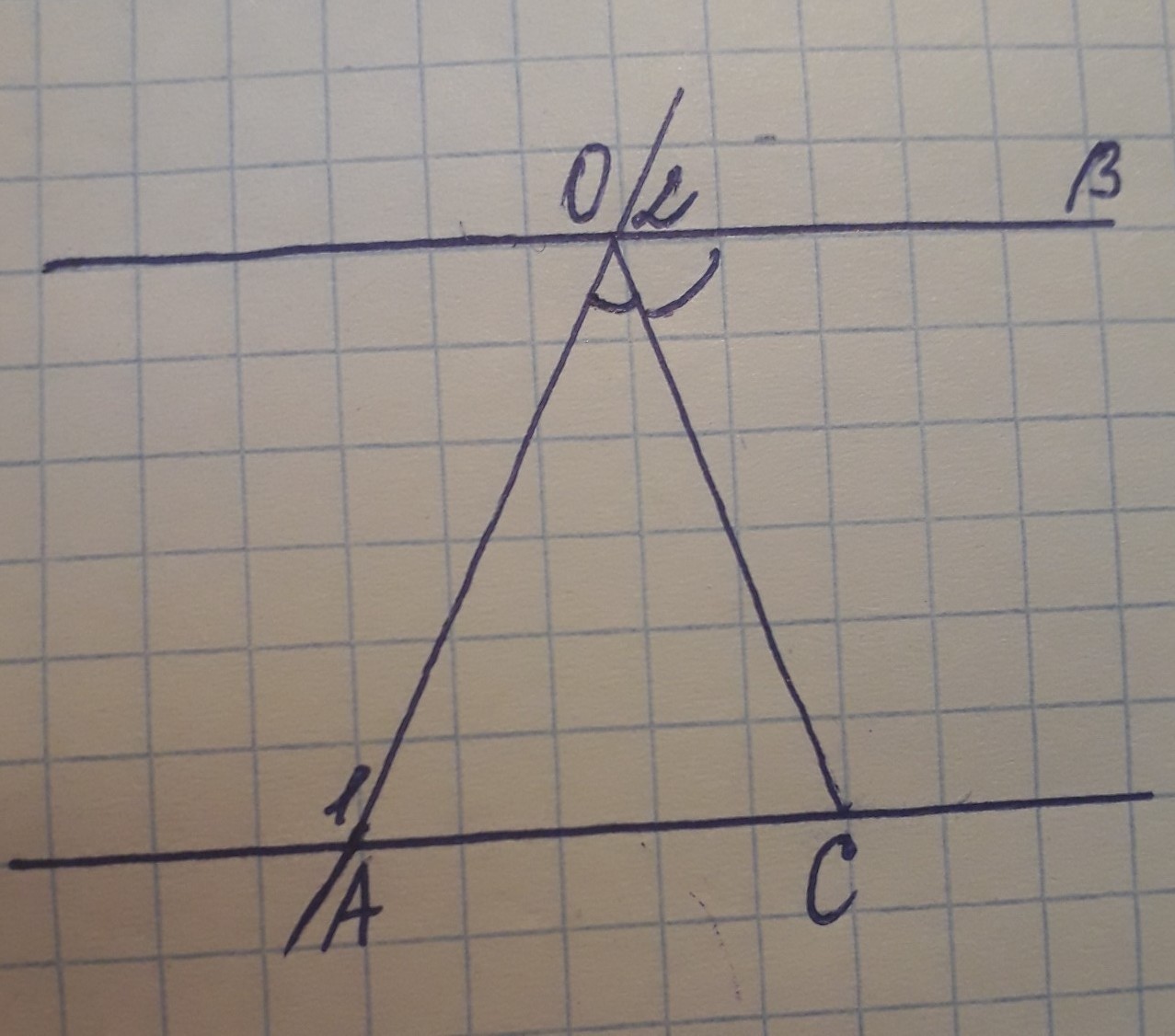
Ответы
Автор ответа:
6
∠АОВ = 180 - ∠2 = 180 - 52 = 128°
∠АОВ = ∠1 ⇒ накрест лежащие углы равны, следовательно ОВ || АС
∠АОС = ∠СОВ = ∠АОВ/2 = 128/2 = 64° (так как ОС - биссектриса)
∠АСО = ∠СОВ = 64° (накрест лежащие углы)
В треугольнике АОС:
∠АОС = ∠АСО = 64° ⇒ ΔАОС равнобедренный, АО = АС, что и требовалось доказать.
daryakartonvezhi:
спасибо❤
Пожалуйста)
Похожие вопросы
Предмет: Алгебра,
автор: vergunmaksim08
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: milanana76
Предмет: Математика,
автор: арбуз554
Предмет: Математика,
автор: 1232068