Предмет: Геометрия,
автор: nika312476
помогите пожалуйста плиииииииииииииз
Приложения:
Ответы
Автор ответа:
1
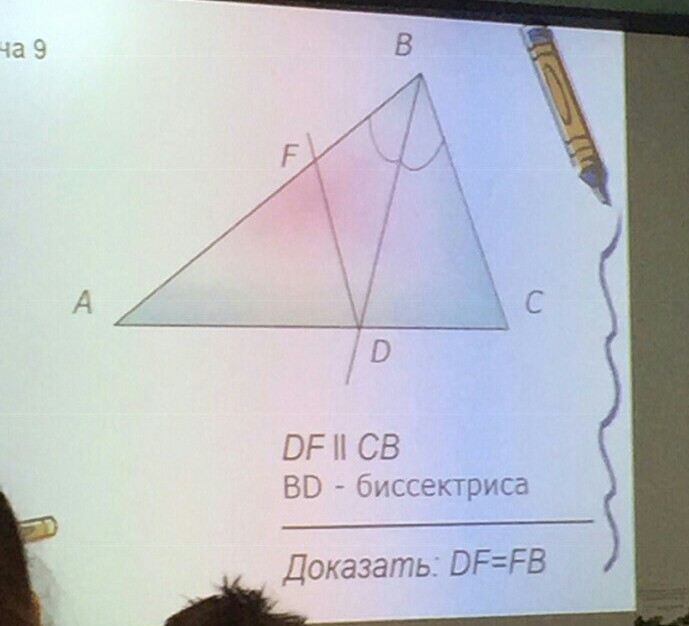
1. Угол СВD и угол BDF равны как внутренние накрест лежащие углы при пересечении DF||CB секущей BD.
2. Угол ABD=углу CBD, угол CBD= углу BDF, значит угол ABD= углу BDF, следовательно ∆DFB равнобедпенный по свойству равнобедренного треугольника, значит DF=FB.
Что и требовалось доказать.
2. Угол ABD=углу CBD, угол CBD= углу BDF, значит угол ABD= углу BDF, следовательно ∆DFB равнобедпенный по свойству равнобедренного треугольника, значит DF=FB.
Что и требовалось доказать.
Автор ответа:
2
DF ║BC, BD - секущая ⇒ ∠DBC = ∠BDF (накрест лежащие)
∠BDF = ∠FBD (т.к. ∠FBD = ∠DBC, а ∠DBC = ∠BDF) ⇒ ΔDFB - равнобедренный
Так как ΔDFB - равнобедренный следует, что DF = FB
Похожие вопросы
Предмет: Литература,
автор: lizavettaant3472
Предмет: Русский язык,
автор: vafinagelusa8650
Предмет: Физика,
автор: AlihanAsya7227
Предмет: Математика,
автор: Космос512
Предмет: Математика,
автор: лерок63