Question

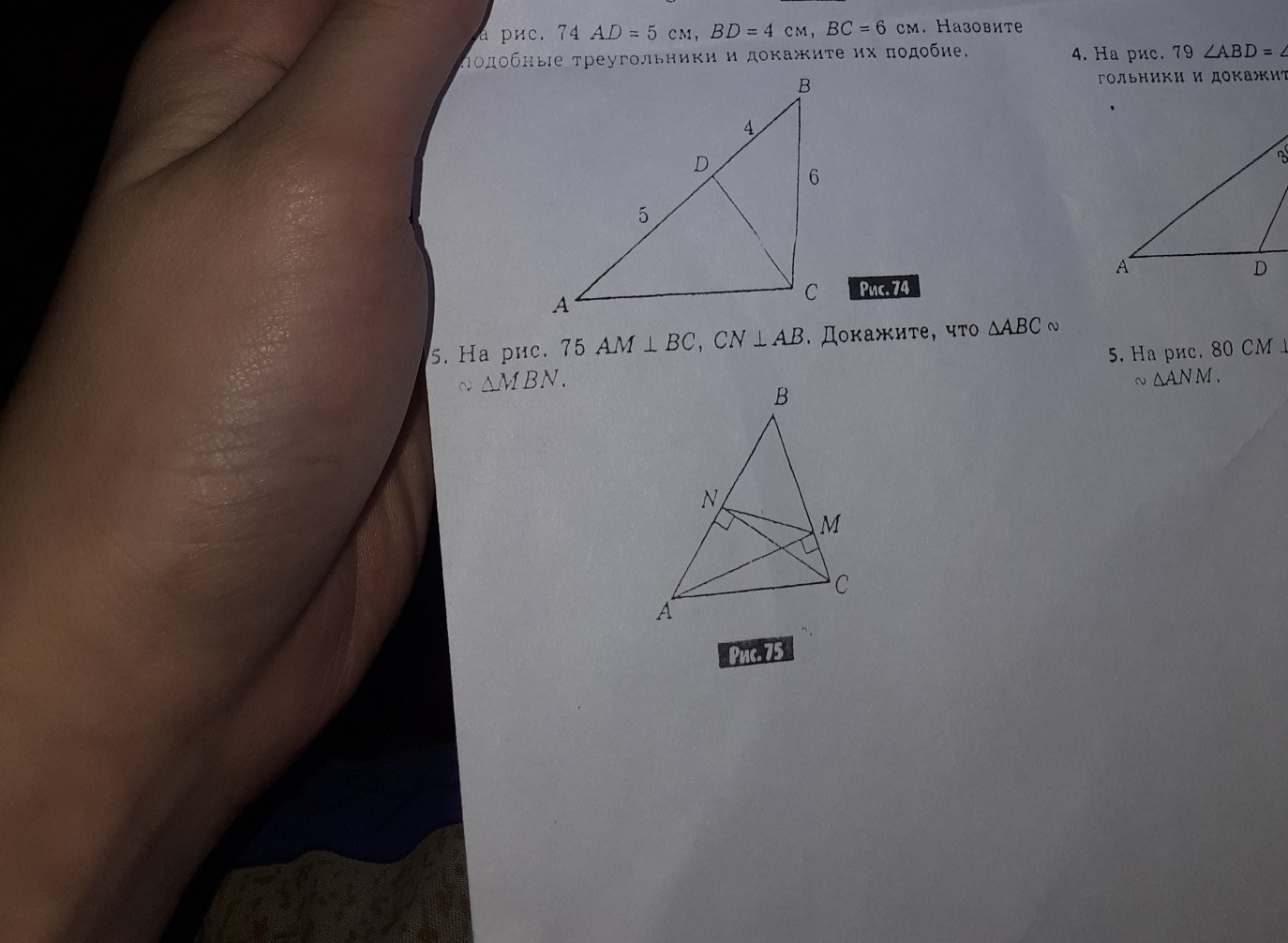
на рисунке 74 AD=5см, BD=4см,BC=6см.Назовите подобные треугольники и докажите их подобие,а по желанию ещё и 75 задачу решите пожалуйста

Answer 1

Ответ:

4. ΔBDC ~ ΔBCA

Объяснение:

4.

BA = BD + AD = 4 + 5 = 9 см

$\dfrac{BC}{BA}=\dfrac{6}{9}=\dfrac{2}{3}$

$\dfrac{BD}{BC}=\dfrac{4}{6}=\dfrac{2}{3}$

Итак, для треугольников BDC и ВСА:

$\dfrac{BC}{BA}=\dfrac{BD}{BC}=\dfrac{2}{3}$

∠В - общий, значит

ΔBDC ~ ΔBCA по двум пропорциональным сторонам и углу между ними.

5.

ΔBCN: (∠BNC = 90°)

        $cosB=\dfrac{BN}{BC}$

ΔBAM: (∠BMA = 90°)

        $cosB=\dfrac{BM}{BA}$

Значит

$\dfrac{BN}{BC}=\dfrac{BM}{BA}$

а так как ∠В общий для треугольников АВС и MBN, то

ΔABC ~ Δ MBN по двум пропорциональным сторонам и углу между ними.