Предмет: Алгебра,
автор: Sola17
помогите решить неравенство
Приложения:
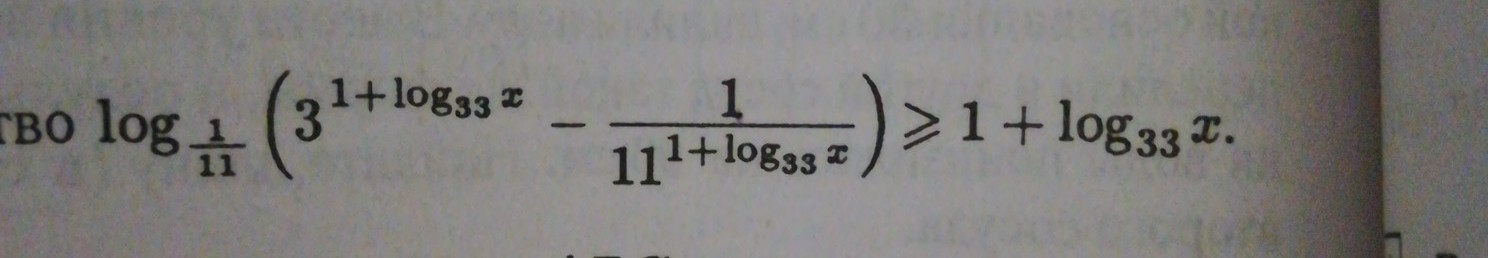
Ответы
Автор ответа:
3
log(1/11) (3^(1 + log(33) x) - 1/11^(1 + log(33) x ) ) ≥ 1 + log(33) x
одз x>0
3^(1 + log(33) x) - 1/11^(1 + log(33) x ) > 0
3^(1 + log(33) x) *11^(1 + log(33) x > 1
33^(1 + log(33) x) > 33^0
1 + log(33) x > 0
x > 1/33
log(1/11) (3^(1 + log(33) x) - 1/11^(1 + log(33) x ) ) ≥ 1 + log(33) x
log(1/11) (3^(1 + log(33) x) - 1/11^(1 + log(33) x ) ) ≥ log(1/11) 1/11^(1 + log(33) x)
3^(1 + log(33) x) - 1/11^(1 + log(33) x ) ≤ 1/11^(1 + log(33) x
3^(1 + log(33) x) - 2/11^(1 + log(33) x ) ≤ 0
(3^(1 + log(33) x)*11(1 + log(33) x) - 2)/11^(1 + log(33) x ) ≤ 0
3^(1 + log(33) x)*11(1 + log(33) x) - 2 ≤ 0
33^(1 + log(33) x) ≤ 2
{ a^log(a) b = b a^(m+n) = a^m*a^n}
33 * x ≤ 2
x≤ 2/33
пересекаем с одз
x∈(1/33 2/33]
Похожие вопросы
Предмет: Русский язык,
автор: i4240901
Предмет: Математика,
автор: nastasubina95
Предмет: Математика,
автор: vikasopilka28
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: vika30aminova1