Предмет: Алгебра,
автор: Hestonic
тема логорифмы, решить неравенсто
Приложения:
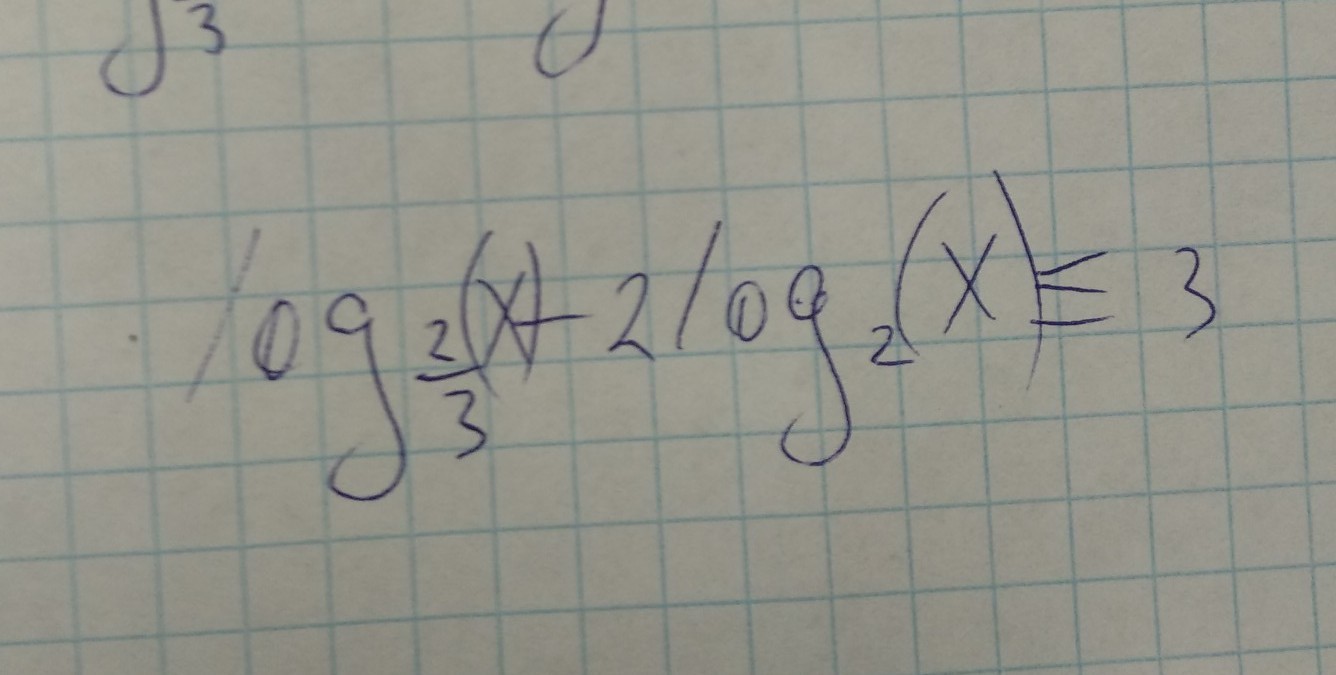
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: anrigorjeladze88
Предмет: История,
автор: vsevolodSerdyukov
Предмет: Математика,
автор: kacenkomariama
Предмет: Алгебра,
автор: олькасоколенко
Предмет: Математика,
автор: dafa3334