Предмет: Алгебра,
автор: Аноним
100 баллов! Не пишите, пожалуйста, фигню, скрины из photomath и тому подобное. Мне нужно решение.
Приложения:
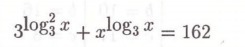
Ответы
Автор ответа:
1
Замена:
Надо ещё заменить x, выразим его по определению логарифма:
Итак, после замены, получаем следующее:
Обратная замена:
Учёт ОДЗ: x>0
Оба корня подходят.
Ответ: 1/9 и 9
Аноним:
Огромнейшее спасибо!!!!!!!
Похожие вопросы
Предмет: Математика,
автор: leronkkaaa13
Предмет: Алгебра,
автор: DianaStreLove
Предмет: Математика,
автор: lousewika
Предмет: Литература,
автор: Iljagorbunov
Предмет: Математика,
автор: камилла190