Предмет: Алгебра,
автор: marimilykh
Алгебра,20 баллов
Найдите значение выражения
Приложения:
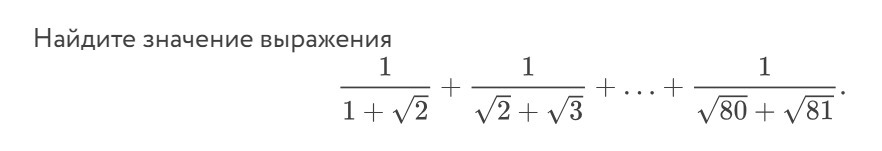
Ответы
Автор ответа:
1
-----------------
Похожие вопросы
Предмет: Русский язык,
автор: dianar2860
Предмет: Другие предметы,
автор: Sophiamusic7279
Предмет: История,
автор: samatovaliana4177
Предмет: Математика,
автор: mikasasusan
Предмет: Математика,
автор: наке3