Постройте вписанно-описанный (бицентрический) четырехугольник и опишите его свойства.
Ответы
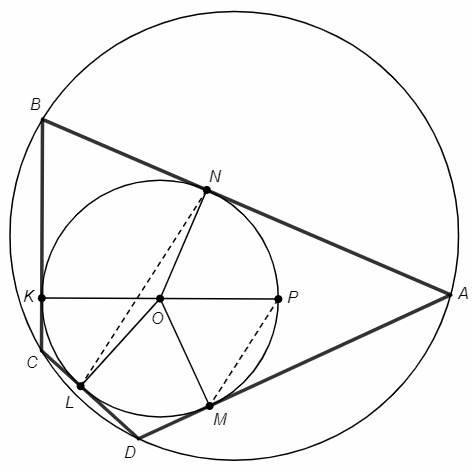
1) Окружность с центром О, диаметр KP.
2) Точки L, M на полуокружности.
3) Прямая LN||MP (точка N на окружности).
4) Касательные через точки K, L, M, N.
Пересечение касательных, проведенных через соседние точки - вершины вписанно-описанного четырехугольника.
Четырехугольник ABCD описанный по построению (стороны являются касательными к окружности).
∠KOL+∠LOP=180 (смежные углы)
∪LM=∪NP (дуги между параллельными LN и MP)
∠LOM=∠NOP => ∠LOP=∠MON => ∠KOL+∠MON=180
В четырехугольниках AMON, CKOL противолежащие прямые углы (касательная перпендикулярна радиусу), следовательно сумма другой пары углов также равна 180.
∠A+∠MON=180, ∠C+∠KOL=180 => ∠A+∠C=180
В четырехугольнике ABCD сумма противолежащих углов равна 180, следовательно он вписанный.
Четырёхугольник является описанным только тогда, когда суммы его противолежащих сторон равны.
Выпуклый четырёхугольник является вписанным только тогда, когда сумма его противолежащих углов равна 180.
Свойства вписанно-описанного четырёхугольника:
a, b, c, d - стороны
S=√(abcd)
R - радиус описанной окружности, r - радиус вписанной окружности, k - расстояние между центрами окружностей.
1/(R+k)^2 +1/(R-k)^2 =1/r^2