Question

Расстояние между центрами окружностей, вписанной и вписанной около прямоугольного треугольника, равно √5. Найдите гипотенузу этого треугольника, если радиус окружности, вписанной в него, равен 2. Помогите пожалуйста!!!

Answer 1

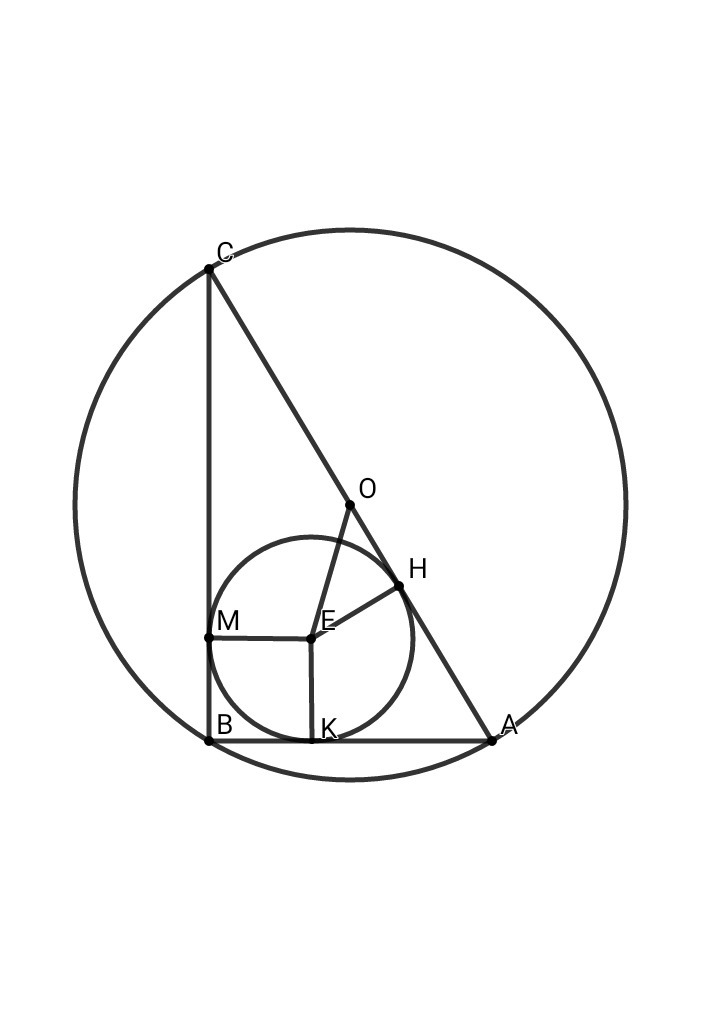
• Рассмотрим ΔОЕН: по т. Пифагора

ОН² = ОЕ² - ЕН² = (√5)² - 2² = 5 - 4 = 1

ОН = 1

• Пусть СО = ОА = х , тогда по свойству отрезков касательных  СН = СМ = СО + ОН = х + 1 , АН = АК = ОА - ОН = х - 1 , ВМ = ВК = 2

• Рассмотрим ΔАВС:  АС = 2х , ВС = СМ + ВМ = х + 1 + 2 = х + 3 , АВ = АК + ВК = х - 1 + 2 = х + 1

По теореме Пифагора:

АС² = ВС² + АВ²

( 2х )² = ( х + 3 )² + ( х + 1 )²

4х² = х² + 6х + 9 + х² + 2х + 1

2х² - 8х - 10 = 0

х² - 4х - 5 = 0  

D = (-4)² - 4•1•(-5) = 16 + 20 = 36

x = (4-6)/2 = -2/2 = - 1 - не подходит по смыслу задачи

x = (4+6)/2 = 10/2 = 5

Значит, АС = 2х = 2•5 = 10

ОТВЕТ: 10

Answer 2

Пусть d - расстояние между центрами вписанной и описанной

окружностей , r и R - их радиусы , тогда имеет место формула

Эйлера :  d² = R² - 2R·r  ,  подставляя в нее данные

задачи , получим :  5 = R² - 4R    или   :

R² - 4R - 5 =0   ⇒   R =5 или R = -1 ,   второй корень

посторонний ⇒ R = 5  , гипотенуза равна диаметру описанной

окружности , то есть равна 10

Ответ :  10

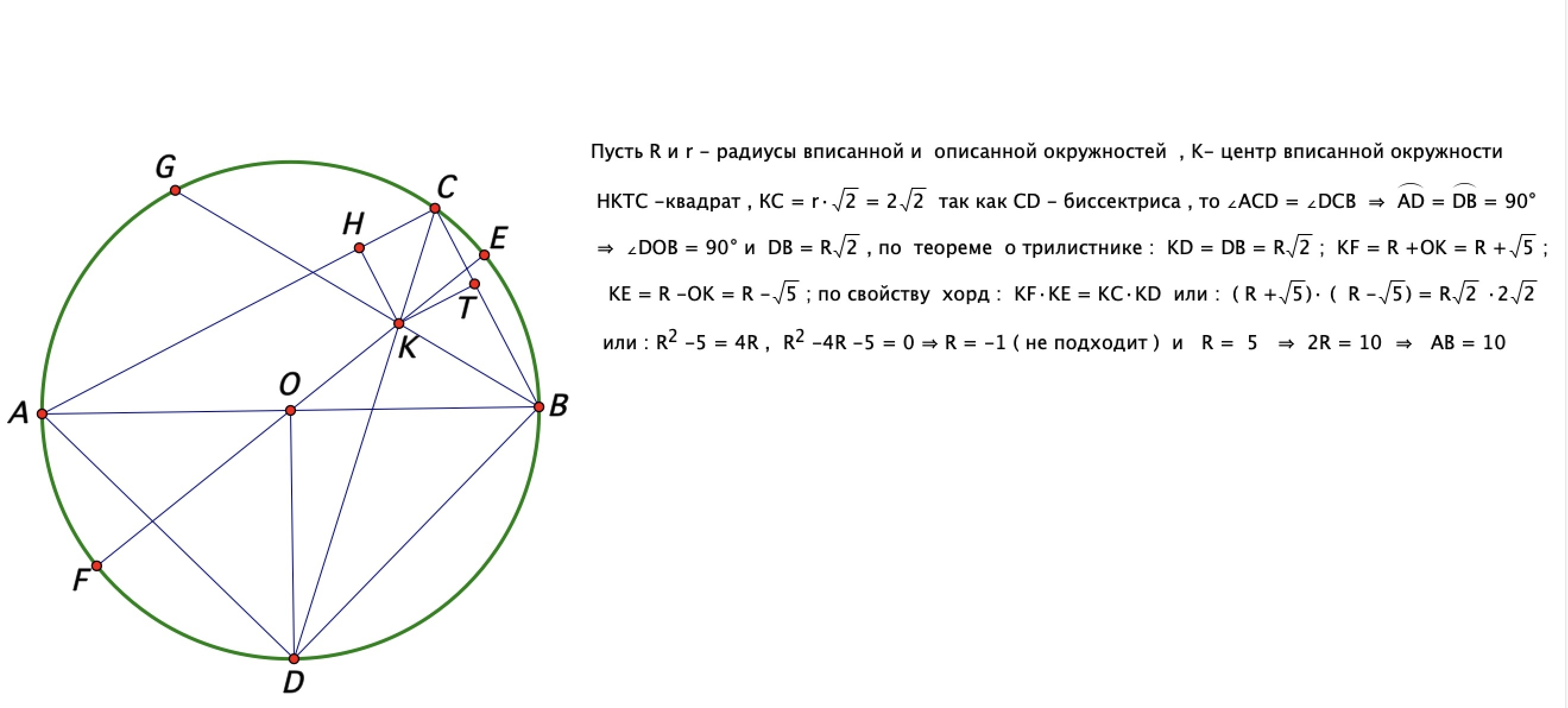
   Еще одно решение :