Предмет: Математика,
автор: skarlett99
как записать интеграл из этого выражения
Приложения:
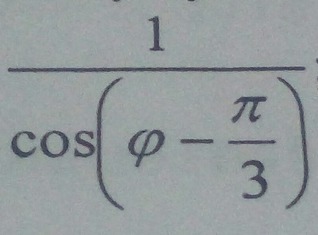
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Судя по всему надо найти длину дуги кривой заданной такой функцией на каком-то интервале.
Для этого находим производную функции
и записываем интеграл от следующего выражения:
skarlett99:
господиииии,спасибо,уже месяц жду помощи
там в задание еще есть продолжение 0≤φ ≤π/2
ну вот их и подставить вместо фи1 и фи2
хорошо,спасибо
Похожие вопросы
Предмет: Информатика,
автор: Mayaaaas
Предмет: Английский язык,
автор: pomoshnik705
Предмет: Английский язык,
автор: Tvirist
Предмет: Алгебра,
автор: Ционисимивирий
Предмет: История,
автор: sasha347347