Question

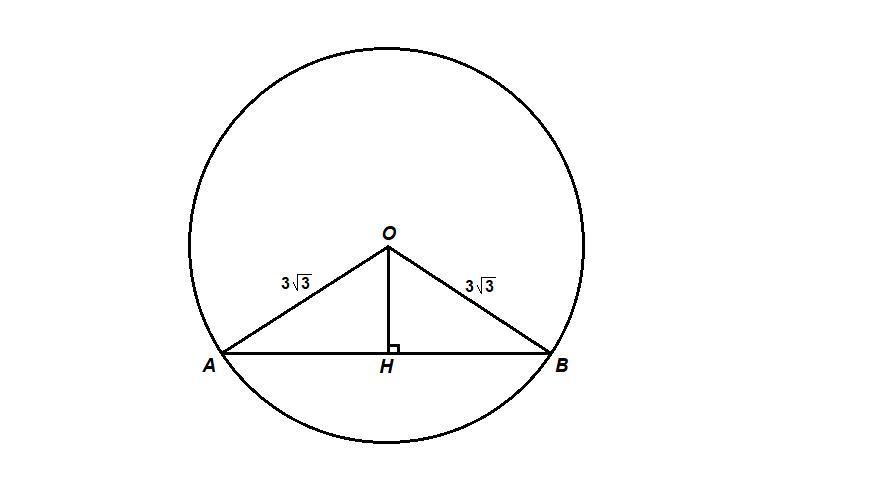
В окружности с центром в точке O и радиусом 3√3 проведена хорда AB так, что угол AOB равен 120°. Найдите длину хорды AB.

Answer 1

Ответ:

AB = 9

Объяснение:

АО = ВО как радиусы, значит ΔАОВ равнобедренный, ⇒

∠ОАВ = ∠ОВА = (180° - ∠АОВ) / 2 = (180° - 120°) / 2 = 60° / 2 = 30°

Проведем ОН - высоту ΔАОВ. Так как треугольник равнобедренный,  то ОН и медиана, АН = НВ.

ΔОАН:  ∠ОНА = 90°,

            $cosOAH=\dfrac{AH}{AO}$

            AH = AO · cosOAH

            $AH=3\sqrt{3}\cdot \dfrac{\sqrt{3}}{2}=\dfrac{9}{2}=4,5$

AB = 2AH = 4,5 · 2 = 9