Исследовать функцию y=f(x) на непрерывность. Найти точки разрыва функции и определить их тип. Построить схематический график функции.
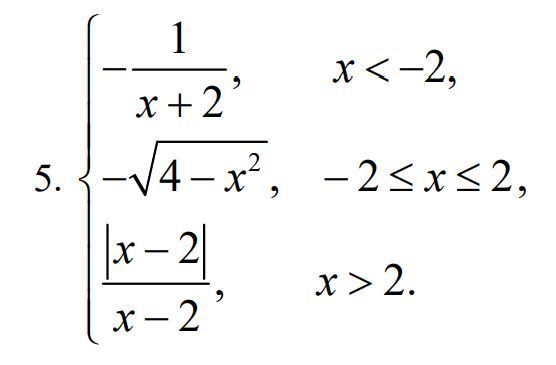
Ответы
Пошаговое объяснение:
Прекрасная кусочно-заданная функция. Точки разрыва? - там где она не существует. Здесь видим два таких события: деление на ноль и корень из отрицательного числа.
Первый участок. Y = - 1/(x+2) и х+2 ≠0 и х≠ -2 - дано.
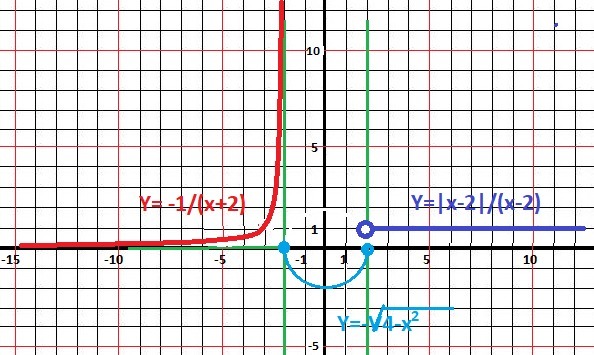
D1(y) - X∈(-∞;-2) - область определения. Делаем участок графика - на рисунке в приложении. Это модификация функции Y = -1/x - ветвь перевёрнута относительно оси ОХ (знак минус) и сдвинута на х=-2 относительно оси ОУ.
Второй участок. Y=-√(4-x²) - это замаскированная отрицательная часть окружности радиуса 2. Проверяем и получаем уравнение:
y² = 4 - x² или x²+y² = 2² - окружность.
ВАЖНО: Функция существует и при Х=-2 и Х=2 - на графике КРУГИ- .
Третий участок. Y = |x-2|/(x-2) при Х>2 превращается в функцию Y = 1 - прямая линий.
ВАЖНО: В точке Х=-2 функция не определена - "дырка" - на графике "кольцо".
График функции на рисунке в приложении, а уж определить тип разрыва оставляю для самостоятельной работы.
У меня в профиле задание..