Question

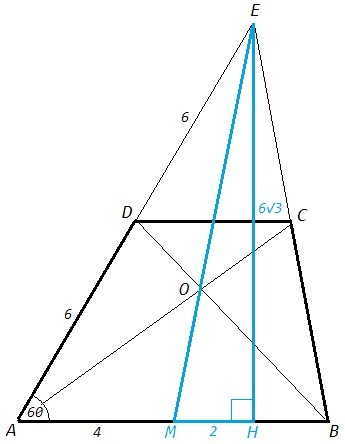
В трапеции АВСD основание АВ в два раза больше основания СD, О
и Е – точки пересечения диагоналей и продолжений боковых сторон соответственно. Найти ОЕ, если АВ = 8, АD = 6, угол DАВ = 60°

Answer 1

CD - средняя линия в △AEB (параллельна основанию и равна его половине), AE=2AD=12.

В трапеции пересечение диагоналей, пересечение продолжений боковых сторон, середины оснований лежат на одной прямой. M - середина AB, AM=AB/2=4.

По теореме косинусов, △EAM:

EM=√(AE^2 +AM^2 -2AE*AM*cos60) =√(12^2 +4^2 -12*4) =4√7

Или

EH - высота на AB. △EAH с углами 60, 90. AH=6, EH=6√3

MH=AH-AM=2

EM=√(EH^2+MH^2) =√(36*3+4) =4√7

Медианы в треугольнике делятся точкой пересечения в отношении 2:1 от вершины. AC, BD, EM - медианы.

OE=2/3 EM =8√7/3