Предмет: Геометрия,
автор: qurmanbek04
На стороне BC треугольника ABC взята точка A1 так, что
BA1 : A1C = 2 : 1. В каком отношении медиана CC1 делит отрезок AA1?
Ответы
Автор ответа:
9
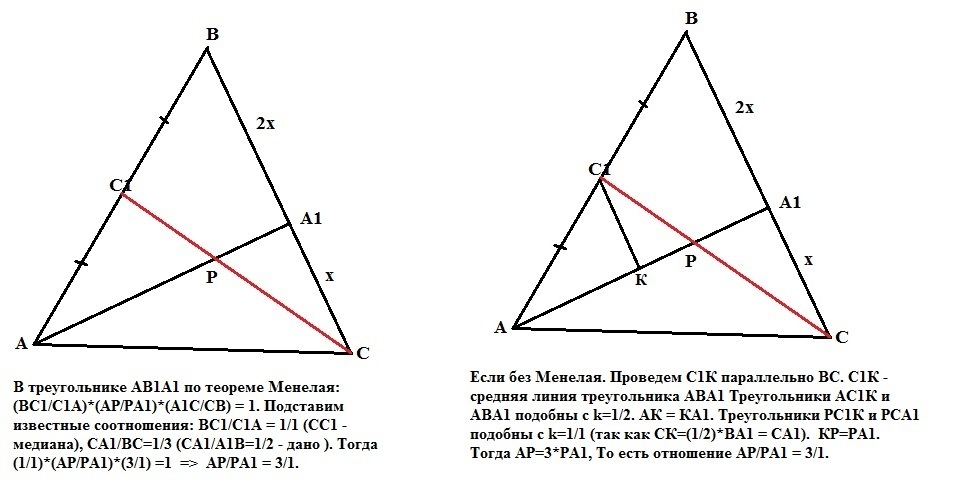
В треугольнике АВ1А1 по теореме Менелая:
(ВС1/С1А)*(АР/РА1)*(А1С/СВ) = 1. Подставим известные соотношения: ВС1/С1А = 1/1 (СС1 - медиана), СА1/ВС=1/3 (СА1/А1В=1/2 - дано ). Тогда (1/1)*(АР/РА1)*(3/1) =1 => АР/РА1 = 3/1.
Ответ: медиана СС1 делит отрезок АА1 в отношении АР:РА1 = 3:1.
Без применения формулы Менелая.
Проведем С1К параллельно ВС. С1К - средняя линия треугольника АВА1, так как точка С1 делит сторону АВ пополам, а отрезок КС1 параллелен стороне ВС по построению. Треугольники АС1К и АВА1 подобны с коэффициентом k=1/2. АК=КА1. Треугольники РС1К и РСА1 подобны с коэффициентом k=1/1 (то есть равны, так как СК=(1/2)*ВА1). КР=РА1.Тогда АР = 3*РА1. То есть отношение АР/РА1 = 3:1.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: romelvladislav29
Предмет: Биология,
автор: mmmmmaik
Предмет: Химия,
автор: den790fr
Предмет: Математика,
автор: viktoriaperegu