Предмет: Алгебра,
автор: vladimirmaslov2017
50б помогите пожалуйста с заданием: сократить дробь
Приложения:
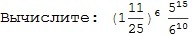
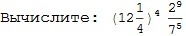

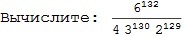
Ответы
Автор ответа:
2
Все-все-все на рисунке
Приложения:


Автор ответа:
2
Похожие вопросы
Предмет: Алгебра,
автор: elizavetaagafonova65
Предмет: Математика,
автор: PretyMary09
Предмет: Русский язык,
автор: twwgp5fkrt
Предмет: Физика,
автор: Ваня1111111113
Предмет: Алгебра,
автор: blackperepeltv