Укажите решение неравенства (х+5)(х-9)>0
Очень нужно
Заранее спасибо❤
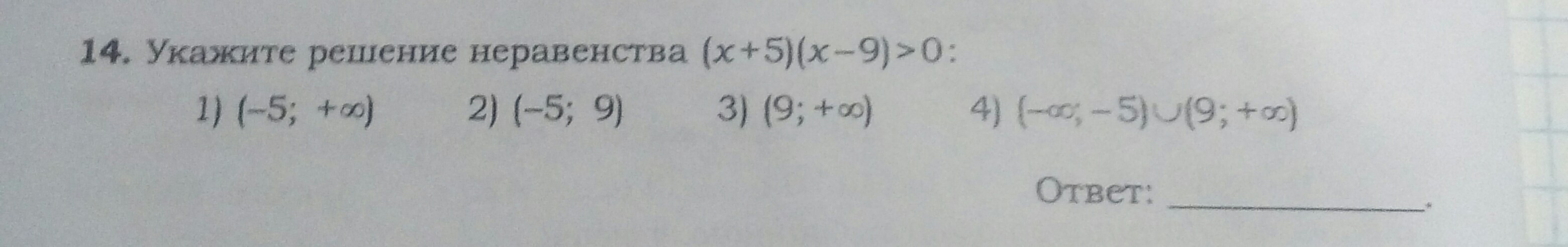
Ответы
Ответ:
4) (-∞; -5)∪(9; +∞)
Объяснение:
(х+5)·(х-9)>0
Применим метод интервалов.
1. Находим нули функции y=(х+5)·(х-9), то есть решаем уравнение:
(х+5)·(х-9)=0 ⇔ х+5=0 или х-9=0 ⇒ x₁ = -5, x₂ = 9.
2. Точки x₁ = -5 и x₂ = 9 делят ось Ох на интервалы (-∞; -5), (-5; 9) и (9; +∞), на каждом из них функция y=(х+5)·(х-9) сохраняет свой знак.
3. Определим знаки функции:
а) -10∈(-∞; -5): y(-10)=(-10+5)·(-10-9)=(-5)·(-19)=95>0, то есть функция положительна;
б) 0∈(-5; 9): y(0)=(0+5)·(0-9)=5·(-9)= -45<0, то есть функция отрицательна;
в) 10∈(9; +∞): y(10)=(10+5)·(10-9)=15·1)=15>0, то есть функция положительна.
4. Ответом будет множество
(-∞; -5)∪(9; +∞)
(х + 5)(х - 9) > 0.
Решим неравенство методом интервалов. Для чего найдем нули функции у = (х + 5)(х - 9), т.е. значения перменной х, для которых значение у = 0:
(х + 5)(х - 9) = 0,
х + 5 = 0 или х - 9 = 0,
х = -5 х = 9.
Нули функции разбиваю область определения функции на 3 промежутка. Выясним знак функции на каждом из промежутков:
+ - +
--------------|---------------------------|------------>
-5 9
x ∈ (-∞; -5) ∪ (9; +∞)
Ответ: 4).