Предмет: Алгебра,
автор: Аноним
Решите пожалуйста лимит, даю максимум баллов.
Приложения:
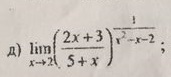
Ответы
Автор ответа:
1
Автор ответа:
1
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ardakmizamhan9
Предмет: Русский язык,
автор: adelamamatalieva111
Предмет: Химия,
автор: wolf20070403
Предмет: Литература,
автор: настя200715
Предмет: Математика,
автор: 190120071