Предмет: Алгебра,
автор: Николай1582
Решение подробно и ответ!
1. Упростить.
2. Доказать, что значение выражения является рациональным числом.
Приложения:
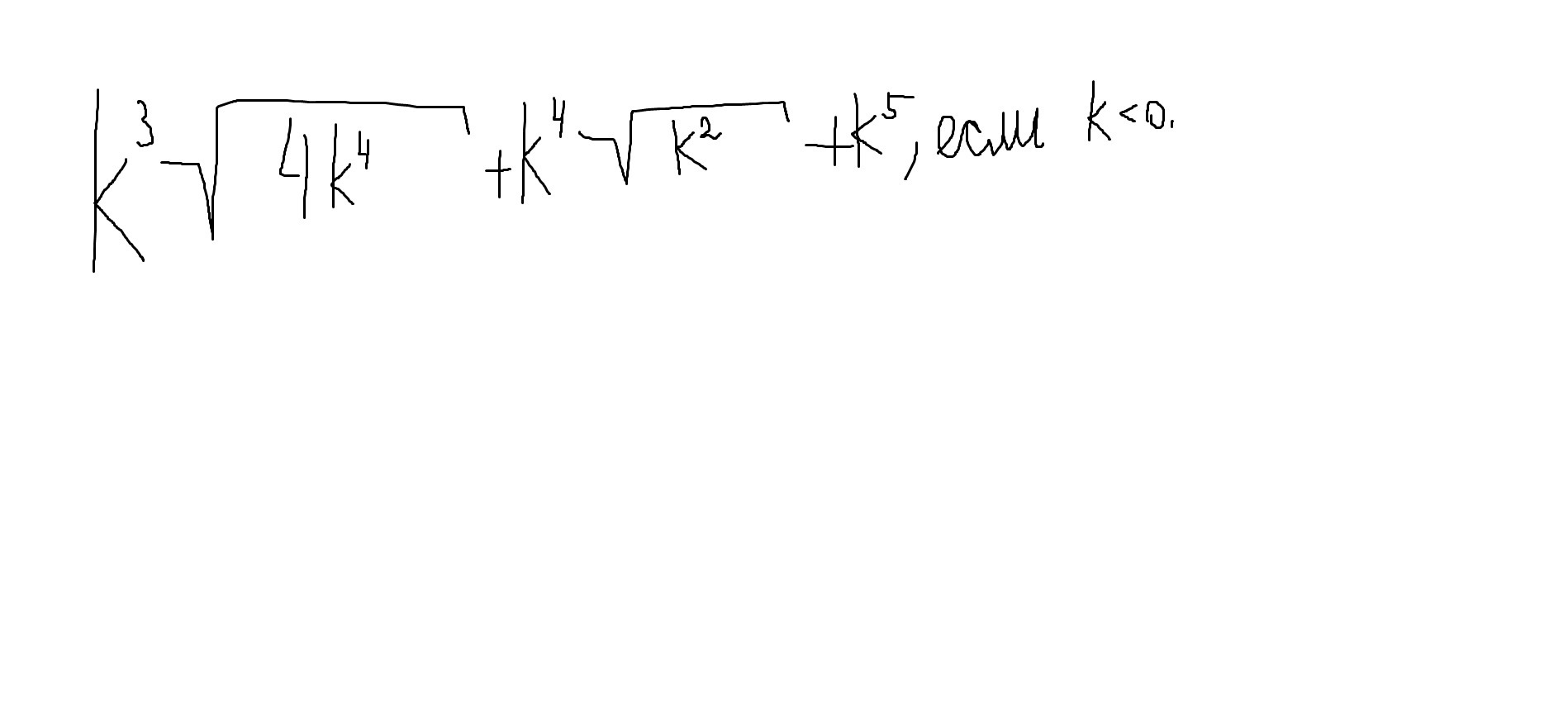
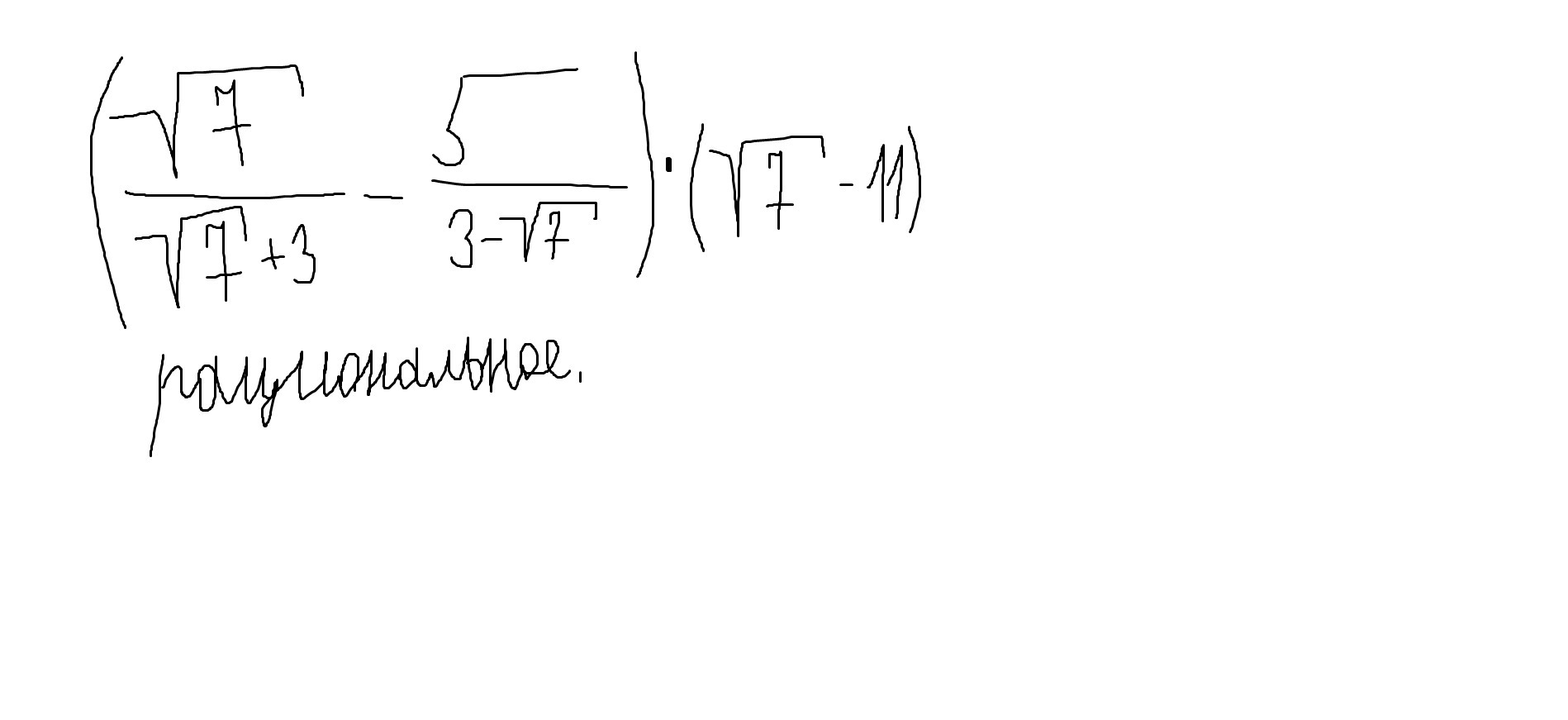
Ответы
Автор ответа:
2
Николай1582:
А почему в 1 примере вместо плюса минус?
Потому что по условию k < 0
А во втором примере почему плюс 22?
Я вынесла минус и поставила перед дробью, знаки в числителе изменились на противоположные.
Спасибо.
Пожалуйста. Если ещё что- то непонятно, спрашивайте.
Похожие вопросы
Предмет: Математика,
автор: kodatskaanna
Предмет: Английский язык,
автор: qwerbel
Предмет: Литература,
автор: marsiik
Предмет: Математика,
автор: AlinaTsurskaya2