Помогите. Срочно! Даю 30 баллов.

Ответы
№2
а) x² ≥ 121
x ≥ 11
Ответ: [11;+∞).
б) x²-2x-8 ≤ 0
x²-2x-8 = 0
D = b²-4ac => (-2²)-4*1*(-8) = 4+32 = √36 = 6 > 0, 2 корня.
x =
x₁ =
x₂ =
Получаем: (x-4)(x+2) ≤ 0
x₁ = 4, x₂ = -2
Ответ: [-2;4].
в) 5x²-4x+21 < 0
D = b²-4ac => (-4²)-4*5*21 = 16-420 = -404<0, нет корней.
Ответ: (-∞;0).
г) (x-2)(x-3)(x+1) > 0
x₁ = 2, x₂ = 3, x₃ = -1
Ответ: (-∞;-1) ∪ (2;3).
д) Не знаю как решать (с баллами обманул конечно)
№3.
Если вставить число p меньше чем требуется, то мы получим нет корней. Смотрим: (Можно 1,2,3, больше уже будут корни)
2x² + 3x + 2 = 0
D = b²-4ac => 3² - 4*2*2 = 9-16 = -7<0, нет корней.
№4
y =
Сначала разберем дискриминант:
x²+6x+8 = 0
D => 6²-4*1*8 = 36-32 = √4 = 2>0, 2 корня.
x₁ =
x₂ =
Получаем:
Конечный вид:
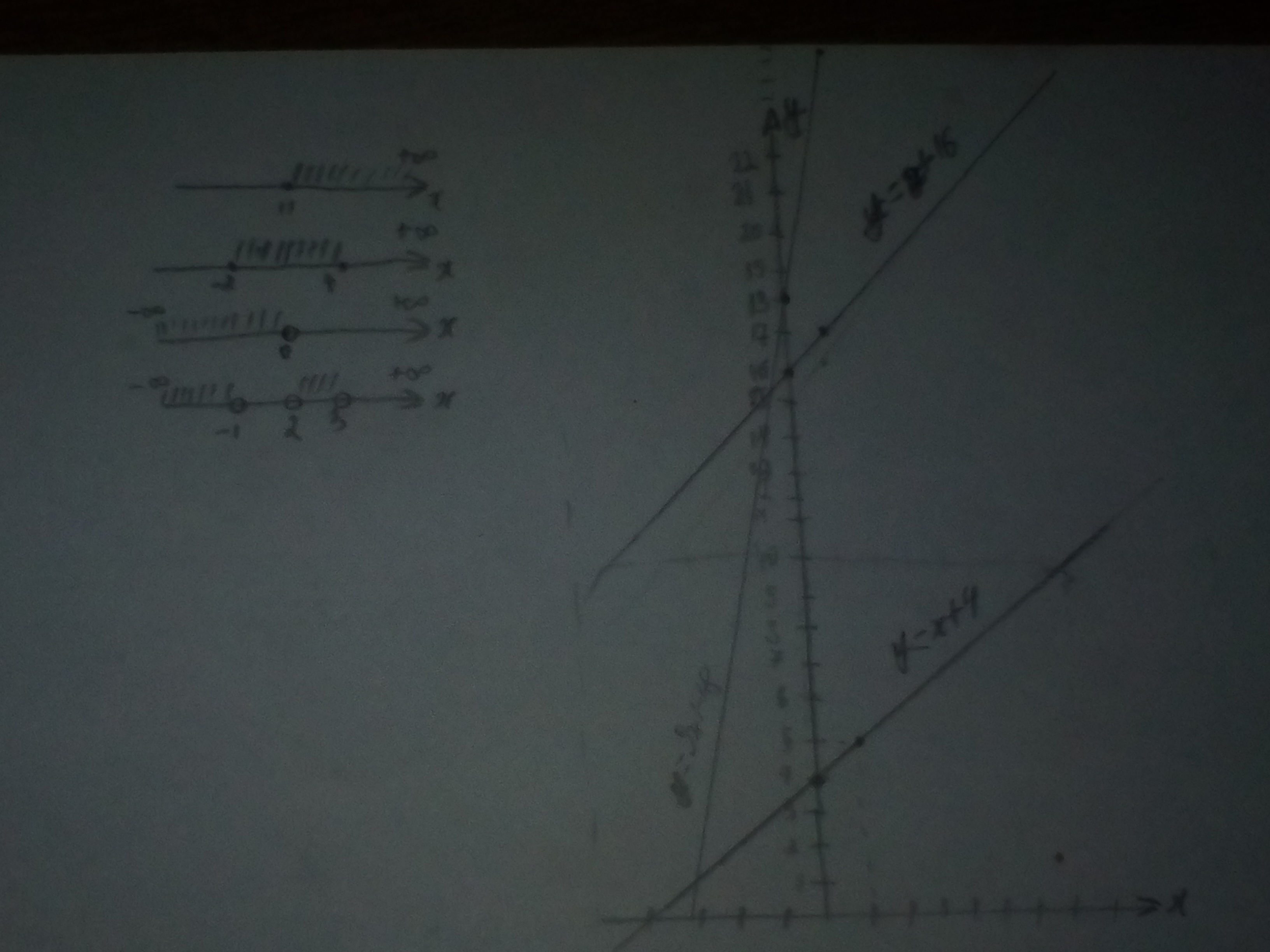
Строим графики по таблице:
1) y = x+4 - линейная функция, графиком является прямая.
x 0 1 x = 0 => y = 0+4 = 4 x = 1 => 1+4 = 5
y 4 5
2) y = x+16 - линейная функция, графиком является прямая.
x 0 1 x = 0 => 0+16 = 16 x = 1 => 1+16 = 17
y 16 17
3) y = 9x+18 - линейная функция, графиком является прямая.
x 0 1 x = 0 => 9*0+18 = 18 x = 1 => 9*1+18 = 27
y 18 27
На фото начерченые три прямые, благодаря графикам решим область определения, то есть D(x), где от -x до x, также 4 фото неравенств, где одна координатная прямая.
Итак, по трём графикам выходит: D(x) = (-∞;+∞).