Предмет: Математика,
автор: smayl1ks
Решить неравенство, дробь 6^(sqrtx) / x+1 > 6^(sqrtx)-1
Приложения:
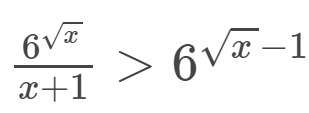
Ответы
Автор ответа:
1
ОДЗ:
Прологарифмируем обе части неравенства (с основанием 6):
С учётом ОДЗ в итоге получаем:
smayl1ks:
"1" не является решением данного неравенства ?
Ой, простите, конечно же -1, сейчас исправлю
Спасибо)
Похожие вопросы
Предмет: Английский язык,
автор: dz099259
Предмет: Математика,
автор: zanina22
Предмет: Русский язык,
автор: shamxalyan2010
Предмет: Химия,
автор: pirat25rus1