Предмет: Математика, автор: 940912

1)1 1/9= 2)2 1/9= 3)-31/9 4)-1/9=

Ответы

Автор ответа: sumaya13q

6

решение и ответ на фотографии☝

Приложения:

Предыдущий вопрос

Следующий вопрос

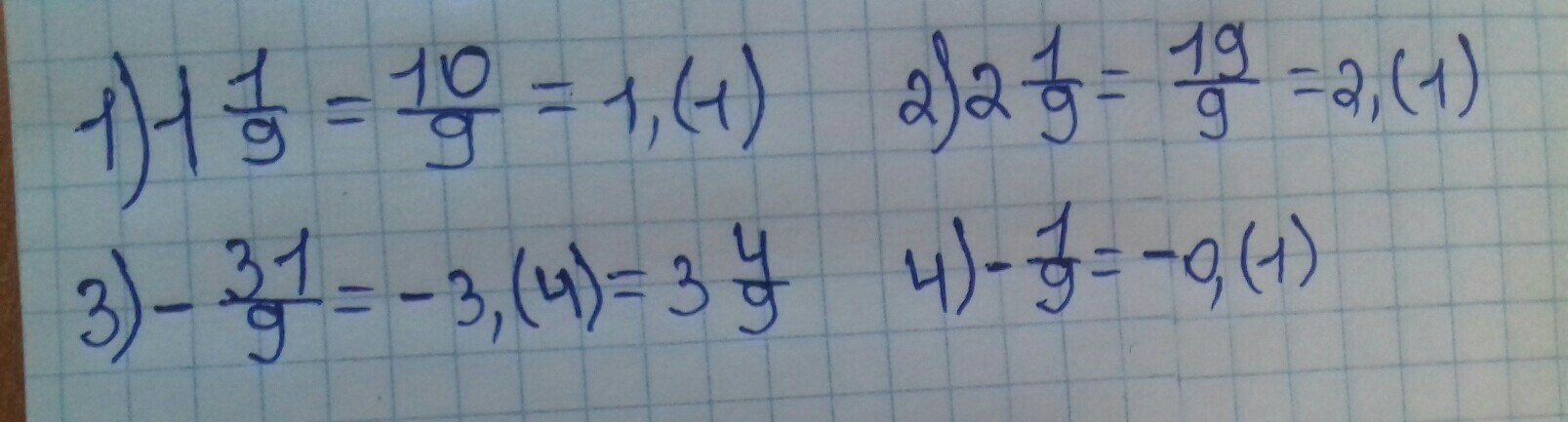
Похожие вопросы

Предмет: Русский язык, автор: Bogdan9669

В предложении притяжательные местоимения чаще всего являются ...
Тема:Личные, возвратные, притяжательные местоимения 6 класс

5 лет назад

Предмет: Геометрия, автор: Eller0

Решите тест, даю 50 баллов 8 класс

1. Два подобных треугольника АВС и А1В1С1 имеют сходственные стороны
1) АВ и СД
2) ВС и В1С1
3) АВ и А1С1
2. Найдите коэффициент подобия треугольников АВС и А1В1С1, если АВ = 12 см, А1В1 =24см
1) 0,05
2) 2
3) 0,5
3. Выберите верное продолжение определения. Два треугольника называются подобными, если *
1) их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
2) их углы соответственно равны и каждая сторона одного треугольника пропорциональна каждой стороне другого треугольника.
3) их углы равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
4. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.Выберите соответствующий номер признака подобия треугольников.
1) Первый
2) Третий
3) Второй
4) Четвертый
5. Три угла одного треугольника соответственно равны трём углам другого треугольника.Такие треугольники подобны по
1)первому признаку подобия
2)определению подобных треугольников
3)третьему признаку подобия
4)второму признаку подобия
6. Стороны одного треугольника равны 15см, 21см, 30см. Две стороны подобного ему треугольника – 10см и 5см. Длина третьей стороны…
1) 3 см
2) 7 см
3) 12 см
4) 10 см
7. Треугольники АВС ~MNK , АВ=4, ВС=6, АС=7, MH=8. Сторона HK равна
1) 3
2) 12
3) 14
4) 3,5
8.Площадь ∆АВС = 120 см2, коэффициент подобия равен 2. Найдите площадь ∆А1В1С1. *
1) 60
2) 240
3) 30
4) 120
9. Найдите периметр треугольника АВС, если у подобного ему треугольника А1В1С1 стороны А1В1 = 12 см, В1С1 = 28 см, А1С1 = 10 см, а коэффициент подобия равен 5.
1) 250
2) 100
3) 10
4) 50
10. Выберите верные утверждения.
1) Любые два квадрата подобны.
2) Любые равнобедренные треугольники, имеющие по равному острому углу, подобны.
3) Любые равнобедренные треугольники, имеющие по равному тупому углу, подобны.
4) Любые прямоугольники подобны.
5) Любые две окружности разного радиуса подобны.

5 лет назад

Предмет: Литература, автор: dianatsiselska29070

Твір на тему—
"Коли збуваються мрії? "
(за повістю"Пурпурові вітрила" О.Гріна.)

5 лет назад

Предмет: Математика, автор: wowa07

решить уравнения
x-52=29
e-46=35
c-24=57
y-37=44

8 лет назад

Предмет: Математика, автор: полиk10

выразите в мм 76 дм 67 см дам 25 балов help me PLEAZ

8 лет назад