Предмет: Алгебра,
автор: pika52
Решите тригонометрические уравнения 3,4,5
Нужно с решением
3) sin 3x sin 2x - cos 3x cos 2x =1
4) 1 - cos x = sin x/2
5) 2cos^2 x + sin x + 1 = 0
Приложения:
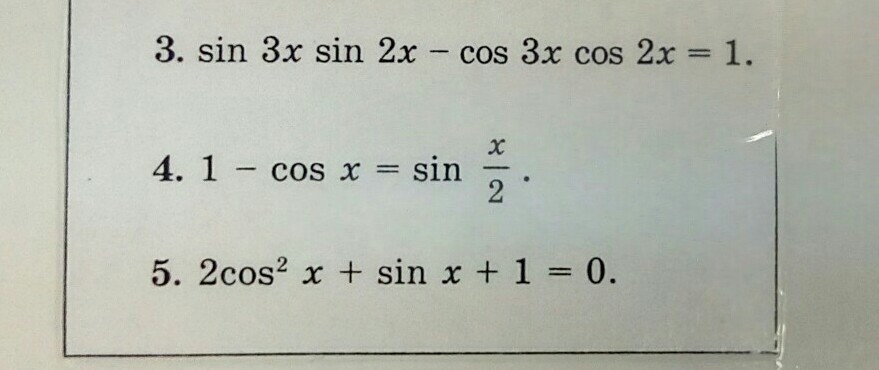
Ответы
Автор ответа:
1
3.
4.
Решаем первое уравнение:
Решаем второе уравнение:
5.
Похожие вопросы
Предмет: Экономика,
автор: askaalex97
Предмет: Русский язык,
автор: Yeoslav55
Предмет: Английский язык,
автор: pogosyankatrina1223
Предмет: Математика,
автор: лина316
Предмет: Геометрия,
автор: tanya360