Question

Решите методом интервалов:
$(x - 5)(x + 3) |x - 6| > 0$

Answer 1

Решить методом интервалов.

Найдём "нули" нашего неравенства:

1) $x-5 = 0 \Rightarrow x = 5.$

2) $x+3 = 0 \Rightarrow x = -3.$

3) $|x-6| = 0 \Rightarrow x = 6.$

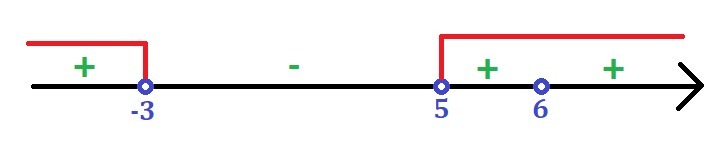
Выделим полученные точки на числовой прямой, они будут "выколотыми" (то есть с дыркой), так как неравенство строгое, эти точки мы не берём.

Рассмотрим каждый интервал. Подставим в неравенство число из этого интервала и пометим полученные знаки.

1) (-∞; -3) ⇒ x = -100 ⇒ - × - × + = +;

2) (-3; 5) ⇒ x = 4 ⇒ - × + × + = -;

3) (5; 6) ⇒ x = 5,5 ⇒ + × + × + = +;

4) (6; +∞) ⇒ x = 100 ⇒ + × + × + = +.

Выделим полученное на прямой. Запишем ответ.

Не забываем, что точка 6 выколота!!

Получаем: x ∈ (-∞; -3) U (5; 6) U (6; +∞).

Ответ: (-∞; -3) U (5; 6) U (6; +∞).