Предмет: Алгебра,
автор: Galinka23
Преобразуйте в произведение
Приложения:
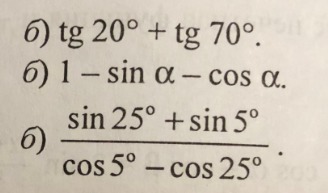
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: География,
автор: Аноним
Предмет: Геометрия,
автор: vertolet12
Предмет: Математика,
автор: batavzdaniiartur
Предмет: Математика,
автор: макс1459